Явление резонанса в цепи переменного тока
Явление резонанса в контуре, состоящем из последовательно соединённых катушки индуктивности , конденсатора и активного сопротивления , заключается в резком возрастании амплитуды вынужденных колебаний силы тока при совпадении циклической частоты генерируемой источником переменной ЭДС с собственной циклической частотой электромагнитных колебаний в контуре:

| Напомним, что частота переменного тока связана с циклической частотой переменного тока простым соотношением: |
Цепь, состоящую из катушки индуктивности, конденсатора и активного сопротивления, соединённых последовательно, сокращенно называют RLC-цепью. Резонанс в RLC-цепи возникает при такой циклической частоте , что реактивное сопротивление катушки становится равным по модулю реактивному сопротивлению конденсатора . Поскольку эти составляющие импеданса RLC-цепи отстоят друг от друга по фазе на (колеблются в противофазе), то компенсируют друг друга, в результате полное сопротивление цепи становится наименьшим, а действующее значение сила тока — наибольшим (здесь — действующее значение напряжения, генерируемого источником переменной ЭДС):
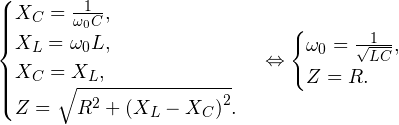
Векторная диаграмма для случая резонанса в цепи переменного тока, состоящей из катушки, конденсатора и активного сопротивления, соединенных последовательно, имеет вид:
Как работает контур колебаний
Работа контура колебаний основана на циклическом преобразовании энергии индуктивности в качественный показатель эффективности конденсатора и наоборот. Допустим, что конденсатор полностью заряжен и энергия, запасенная в нем, максимальна. При подключении его к катушке индуктивности, он начинает разряжаться. При этом, через индуктивность начинает протекать ток, вызывающий появление ЭДС самоиндукции, направленную на уменьшение протекающего тока. Это означает, что начинается процесс перезарядки конденсатора. В тот момент, когда энергия прибора становится равной нулю, та же величина для катушки максимальна.
Далее, энергия индуктивности снижается, расходуясь на заряд емкости с противоположной полярностью. После уменьшения показателя коэффициента самоиндукции до нуля, на конденсаторе она опять имеет максимальное значение.
Вам это будет интересно Особенности системы уравнения
Процессы в системе
Важно! В идеальном случае, данный процесс способен протекать бесконечно. В реальных устройствах колебание затухает со скоростью, пропорциональной потерям в цепи проводников
Вне зависимости от величины энергии, наличия потерь, частота колебаний постоянна и зависит только от значений параметров коэффициента самоиндукции и емкости. Данная величина называется резонансной. Формула резонанса учитывает значение величины емкости и индуктивности контура колебаний.
Осциллограмма
При воздействии на электрическую цепь с катушкой внешним сигналом с частотой, равной резонансной, амплитуда изменения положения частиц резко возрастает. Резонанс отсутствует при несовпадении частот. Из-за предельных значений электрическую цепь с катушкой индуктивности часто называют резонансной.
Потери в цепи с катушкой индуктивности (потери в диэлектрике конденсатора, сопротивление самого устройства, соединительных проводов) ограничивают величину предельных изменений направления частиц. В следствие этого, введена характеристика электроцепи, именуемая добротностью. Добротность обратно пропорциональна предельной величине потерь.
Зависимость предельной частоты от добротности
Важно! Снижение добротности приводит к тому, что предел изменения направлений наступает не только на основной частоте, но и на некотором приближении к ней, то есть, в некоторой полосе частот, где резонансное значение находится посередине. Чем выше добротность, тем более узкой становится полоса частот
ЦЕНТР СВЕТОЛЕЧЕНИЯ
- Прайс-лист
- АИР (урологические процедуры для мужчин)
- ВЛОК (внутривенное лазерное облучение крови)
- Ионофорез
- Консультативный, диагностический приём
- Лечение акне
- Лечение алопеции, стимуляция роста волос
- Лечение асимметрии, сухости губ
- Лечение возрастного увядания кожи
- Лечение гипергидоза
- Лечение гиперпигментации
- Лечение дермальных заломов
- Маски
- Пилинг
- Плазмолифтинг
- Плазмотерапия
- ПР-расческа (Дермалайт 80)
- Светофототерапия (лечение кожных заболеваний)
- Удаление бородавок, фибром, папиллом, невусов др. криодиструкцией
- Удаление бородавок, фибром, папиллом, невусов др. радионожем
- Услуги манипуляционного кабинета
- Цифровая видеодерматоскопия (карта родинок)
Виды общественного резонанса
Реакция людей на события может носить естественный характер, когда большое количество граждан по ряду причин реагирует на него одинаково. В этом случае у человека формируется своя точка зрения или он придерживается мнения большинства, услышанного им во время разговоров, обмена информацией. Такого рода общественное мнение можно наблюдать в небольших коллективах или населенных пунктах.
Но в большинстве случаев, используя возможности современной массовой информации, идет манипулирование мнением множества людей. Здесь уместно будет говорить об управляемом общественном резонансе. Это в некоторых случаях может представлять собой, своего рода, психологическое оружие, способное нанести вред обществу, государству.
Механические колебания маятника
Самая простая модель, которая может наглядно показать колебания, это простейший маятник, а точнее математический маятник. Колебания разделяют на свободные и вынужденные. Первоначально воздействующая энергия на маятник обеспечивает в теле свободные колебания без присутствия внешнего источника переменной энергии воздействия. Данная энергия может быть как кинетической, так и потенциальной.
Здесь не имеет значение насколько сильно или нет качается сам маятник, — время, потраченное на прохождения его пути в прямом и обратном направлении, сохраняется неизменным. Во избежание недоразумений с затуханием колебаний вследствие трения о воздух стоит выделить, что для свободных колебаний должны соблюдаться условия возврата маятника в точку равновесия и отсутствия трения.
А вот частота в свою очередь напрямую зависит от величины длины нити маятника. Чем короче нить, тем выше частота и наоборот.
Возникающая естественная частота тела под воздействием первоначально приложенной силы называется резонансной частотой.
Все тела, которым свойственны колебания, совершают их с заданной частотой. Для поддержания в теле незатухающих колебаний необходимо обеспечить постоянную периодическую энергетическую «подпитку». Это достигается воздействием в одновременный такт колебаний тела постоянной силы с определенным периодом. Таким образом возникающие колебания в теле под действием периодической силы снаружи называют вынужденными.
В какой-то момент внешних воздействий возникает резкий скачок амплитуды. Такой эффект возникает если периоды внутренних колебаний тела совпадают с периодами внешней силы и называется резонансом. Для возникновения резонанса достаточно совсем небольших величин внешних источников воздействия, но с обязательным условием повторения в такт. Естественно, при фактических расчетах в земных условиях не стоит забывать о действии сил трения и сопротивления воздуха на поверхность тело.
Резонанс токов
Резонанс токов
1. Для контура (рис. 5.31) параметры которого равны: 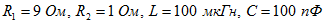 определить, чему равны эквивалентные резистивное, реактивное и полное сопротивления контура, если вследствие расстройки частота станет на 0,2% больше резонансной. Для этого случая вычислить все токи и мощность, выделяемую полагая, что значение приложенного к цепи осталось прежним (U=200 В).Решение:
определить, чему равны эквивалентные резистивное, реактивное и полное сопротивления контура, если вследствие расстройки частота станет на 0,2% больше резонансной. Для этого случая вычислить все токи и мощность, выделяемую полагая, что значение приложенного к цепи осталось прежним (U=200 В).Решение:
Вначале определим добротность Q и сопротивление контура при резонансе:

Произведем расчеты при . Найдем абсолютную и обобщенную расстройки и искомые сопротивления: имеет емкостный характер, так как x, положительно.Полное сопротивление при расстройке
имеет емкостный характер, так как x, положительно.Полное сопротивление при расстройке
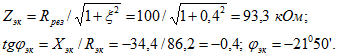
Так как отрицательно, ток опережает напряжение
Расходуемая мощность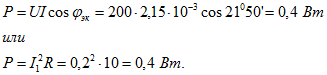
Заметим, что даже при небольшой расстройке (0,2%) в полном сопротивлении контура появилась значительная реактивная составляющая , вследствие которой и оказался сдвиг фаз между током I и напряжением U. Ввиду небольшого изменения частоты реактивные сопротивления каждой из параллельных ветвей и токи в них почти не изменились и не намного изменился ток в неразветвленной части цепи.2. Параллельный контур с малыми потерями (т. е. Q>>1) включен к источнику с ЭДС Е=200 В и внутренним сопротивлением (см. рис. 5.35). Определить параметры контура R и L, если известны резонансная частота , емкость С=300 пФ и что сопротивление контура при резонансе равно внутреннему сопротивлению генератора . Вычислить токи источника, каждой из ветвей, мощность, доставляемую источником, и выделяемую в нем и в параллельном контуре при резонансе.Решение:
Находим индуктивность:
Имея в виду, что по условию находим резистивное сопротивление
Ток источника и напряжение на параллельном контуре при резонансе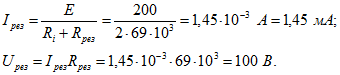
В каждой из ветвей контура токи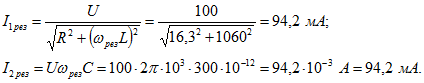
Мощность, доставляемая источником , расходуемая в нем и выделяемая в контуре :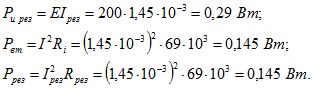
3. Для задачи 2. определить абсолютное значение и относительную величину полосы пропускания контура по напряжению.Решение:
Предварительно вычислим характеристическое сопротивление и добротность контура
Искомые значения абсолютной и относительной величины полосы пропускания контура по напряжению равны: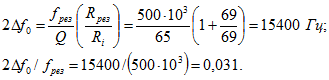
4. Параллельный контур, параметры которого , подключен к источнику с ЭДС Е=200 В и внутренним сопротивлением .1. Вычислить эквивалентную добротность контура и полосу его пропускания. Найти все токи и расходуемую в контуре мощность при резонансе.2. Чему равны эквивалентная добротность контура и полоса его пропускания, если его нагрузить на резистивное сопротивление (рис. 5.41, а)? Определить для данного случая токи, мощности, доставляемую источником и расходуемую в контуре и нагрузочном сопротивлении при резонансе.
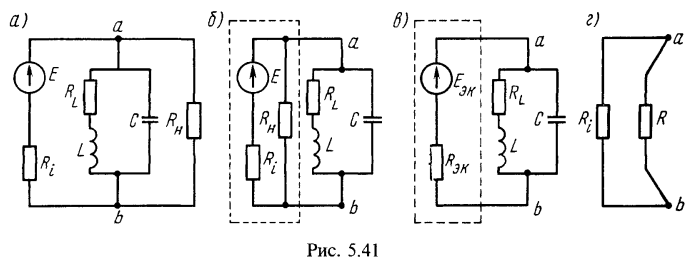
Решение:
1. Для заданного контура вычисляем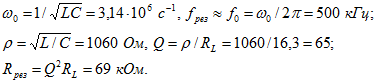
Эквивалентную добротность заданного контура с учетом внутреннего сопротивления источника ЭДС и полосу его пропускания определяем: 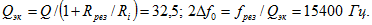 Так как данные контура, ЭДС источника и его внутреннего сопротивления те же, что и в задаче 2., то в решении были уже вычислены требуемые по условию 2. Решение задачи в случае нагрузки контура на сопротивление проще всего получить, осуществив замену относительно зажимов ab заданного источника ЭДС с и подключенным к нему параллельно сопротивлением (рис. 5.41, б), эквивалентным с ЭДС и внутренним сопротивлением (рис. 5.41,в). Для определения отключим параллельный контур (см. рис. 5.41,б и в) и вычислим напряжение холостого хода равное :
Так как данные контура, ЭДС источника и его внутреннего сопротивления те же, что и в задаче 2., то в решении были уже вычислены требуемые по условию 2. Решение задачи в случае нагрузки контура на сопротивление проще всего получить, осуществив замену относительно зажимов ab заданного источника ЭДС с и подключенным к нему параллельно сопротивлением (рис. 5.41, б), эквивалентным с ЭДС и внутренним сопротивлением (рис. 5.41,в). Для определения отключим параллельный контур (см. рис. 5.41,б и в) и вычислим напряжение холостого хода равное :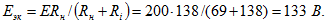
Сопротивление короткого замыкания равно внутреннему сопротивлению эквивалентного источника (рис. 5.41,г):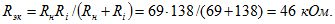
Для схемы рис. 5.41 эквивалентные добротность и полоса пропускания соответственно равны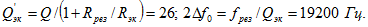
Следует отметить, что подключение к контуру сопротивления приводит к уменьшению эквивалентной добротности и увеличению полосы пропускания.Рассчитываем ток в неразветвленной части заданной цепи, напряжение на контуре, токи в ветвях контура и нагрузочном сопротивлении , мощности, доставляемую источником и выделяемую в контуре и сопротивлении :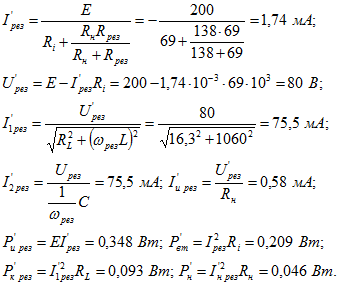
Проверка показывает, что
Смотри полное содержание по представленным решенным задачам.
Примеры
Один знакомый пример – колебание детской площадки, которое действует как маятник. Подталкивание человека в колебании вовремя с естественным интервалом колебания (его резонирующая частота) заставит колебание повыситься и выше (максимальная амплитуда), в то время как попытки выдвинуть колебание в более быстром или более медленном темпе приведут к меньшим дугам. Это вызвано тем, что энергия, которую поглощает колебание, максимизируется, когда толчки «в фазе» с естественными колебаниями колебания, в то время как часть энергии колебания фактически извлечена противостоящей силой толчков, когда они не.
Резонанс происходит широко в природе и эксплуатируется во многих искусственных устройствах. Это – механизм, которым фактически произведены все синусоидальные волны и колебания. Много звуков, которые мы слышим, такой как тогда, когда твердые объекты металла, стекло или древесина поражено, вызваны краткими резонирующими колебаниями в объекте. Свет и другая короткая длина волны электромагнитная радиация произведены резонансом на уровне атомов, таком как электроны в атомах. Другие примеры:
- Хронометрируя механизмы современных часов и часов, например, балансир в механических часах и кварцевый кристалл в кварце наблюдают
- Приливный резонанс Залива Фанди
- Акустические резонансы музыкальных инструментов и человеческих голосовых связок
- Разрушение кристаллического бокала, когда выставлено музыкальному тону правильной подачи (ее резонирующая частота)
- Электрический резонанс настроенных схем в радио и телевизоры, которые позволяют радиочастотам быть выборочно полученными
- Создание когерентного света оптическим резонансом в лазерной впадине
- Орбитальный резонанс, как иллюстрируется некоторыми лунами газовых гигантов солнечной системы
- Материальные резонансы в уровне атомов – основание нескольких спектроскопических методов, которые используются в физике конденсированного вещества
Параметры и электрические величины при резонансе
Теперь давайте по порядку выведем значения параметров и электрических величин при резонансе параллельной цепи RLC.
Резонансная частота
Мы знаем, что резонансная частота f r
— это частота, на которой возникает резонанс. В параллельной RLC цепи резонанс возникает, когда мнимый член допуска Y равен нулю. т.е. значение frac1XC− frac1XL должно быть равно нулю
Rightarrow frac1XC= frac1XL
RightarrowXL=XC
Вышеуказанное условие резонанса такое же, как и в последовательной цепи RLC. Таким образом, резонансная частота f r
будет одинаковой как в последовательной RLC-цепи, так и в параллельной RLC-схеме.
Следовательно, резонансная частота f r
параллельной RLC-схемы равна
fr= frac12 pi sqrtLC
Куда,
- L — индуктивность индуктора.
- С — емкость конденсатора.
Резонансная частота f r
параллельной цепи RLC зависит только от индуктивностиL и емкостиC. Но это не зависит от сопротивленияR.
впуск
Мы получили допуск Y
параллельной цепи RLC как
Y= frac1R+j lgroup frac1XC− frac1XL rgroup
Замените XL=XC в приведенном выше уравнении.
Y= frac1R+j lgroup frac1XC− frac1XC rgroup
RightarrowY= frac1R+j(0)
RightarrowY= frac1R
При резонансе вход
Y параллельной цепи RLC равен обратной величине сопротивления R. т.е. mathbf mathitY= frac1R
Напряжение на каждом элементе
Замените frac1XC− frac1XL=0 в уравнении 1
I=V
RightarrowI= fracVR
RightarrowV=IR
Следовательно, напряжение
на всех элементах параллельной цепи RLC при резонансе равноV = IR .
При резонансе допуск параллельной цепи RLC достигает минимального значения. Следовательно, максимальное напряжение
присутствует на каждом элементе этой цепи в резонансе.
Ток, протекающий через резистор
Ток, протекающий через резистор
IR= fracVR
Подставим значение V
в приведенное выше уравнение.
IR= fracIRR
RightarrowIR=I
Следовательно, ток, протекающий через резистор
в резонансе, составляет mathbf mathitIR=I.
Ток, протекающий через индуктор
Ток, протекающий через индуктор
IL= fracVjXL
Подставим значение V
в приведенное выше уравнение.
IL= fracIRjXL
RightarrowIL=−j lgroup fracRXL rgroupI
RightarrowIL=−jQI
Следовательно, ток, протекающий через индуктор
в резонансе, равен IL=−jQI.
Итак, величина
тока, протекающего через индуктор в резонансе, будет
$$ | I_L | = QI $$
Где Q — фактор качества,
а его значение равно fracRXL
Как используется
Резонансные токи используются сегодня в некоторых фильтрующих системах, радиотехнике, электричестве, радиостанциях, асинхронных двигателях, высокоточных электрических сварных установках, колебательных генераторных электрических контурах и высокочастотных приборах. Нередко, когда они применяются, чтобы снизить генераторную нагрузку.
Обратите внимание! Простейшая цепь, где наблюдаются они, это параллельного вида колебательный контур. Такие контуры используются в современном промышленном индукционном котловом оборудовании и улучшают показатели КПД. Сфера применения
 Сфера применения
Сфера применения
Кварцевые резонаторы и электромеханические фильтры
Это наиболее распространённые резонаторы, включающие в себя кристаллы кварца. Кристалл вырезается в форме параллелепипеда. На полученную пластину в вакууме напыляют электроды. Способы колебаний такого элемента зависят от следующих позиций:
- вида пластины из кварца;
- конструктивного исполнения электродов;
- метода присоединения электродов.
На величину собственной частоты кварцевого резонатора влияют: форма, размеры, модуль упругости и плотность пьезоэлектрического элемента, а также особенности крепления детали.
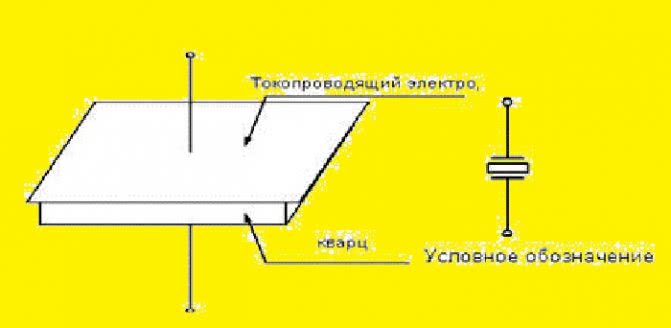
Простейшая конструкция кварцевого резонатора
Электромеханические фильтры (ЭМФ) выполняют ступенчатое преобразование. На первой ступени происходит превращение электрических пульсаций в колебания механической природы. Вторая ступень их фильтрует, третья – снова возвращает в электрическую форму.
Внимание! Вторая ступень – это механический резонатор, он работает как фильтр. Изготавливается из ферритов с магнитострикционными свойствами, кварца, сплавов железа с никелем, пьезокерамических элементов и иных компонентов. Блок-схема ЭМФ
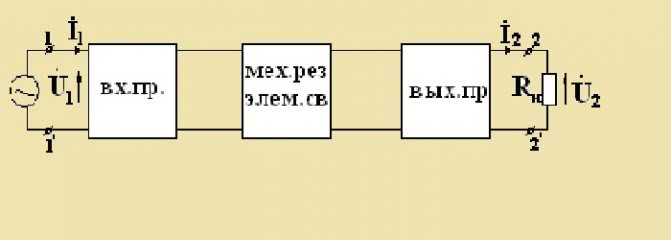
Блок-схема ЭМФ
В чем заключается явление резонанса напряжений
Как известно, в сети переменного тока домашней сети разность потенциалов изменяется с частотой 50 Гц. То есть, каждую секунду производится 50 полных колебаний. Такое явление несложно замерить даже бытовым частотомером, который определить точное значение этого параметра именно по эффекту электромагнитного поля, образованного вокруг проводника с током. Катушка с металлическим сердечником, которая устанавливается в измерительный прибор, будет колебаться с частотой электромагнитного поля домашней электросети.
Вам это будет интересно Особенности SMD маркировки
Частотомер
Таким образом, вырабатывается переменное напряжение, которое затем может быть увеличено, а его частота подсчитана микропроцессорным либо аналоговым устройством, после чего информация может быть выведена на экран.
Разобравшись, в чем заключается явление резонанса электрического напряжения, необходимо стараться всячески избегать этого явления, когда одновременные колебательные движения полей являются нежелательными. Если же в каком-либо устройстве такой эффект применяется с целью получения определенных физических явлений, то схема должна быть изготовлена с высокой добротностью, чтобы на поддержание процесса тратилось как можно меньше энергии (таким образом повышается КПД устройства).
Шпаргалки по электротехнике и электронике — Понятие о резонанс токов
Sunday, 24 January 2016 04:20
administrator
| Cмотрите так же… |
|---|
| Шпаргалки по электротехнике и электронике |
| Закон Ома для замкнутой цепи и для участка цепи |
| Законы Кирхгофа для цепи постоянного тока |
| Расчет простых цепей при различных схемах соединения потребителей |
| Понятие о сложной электрической цепи |
| Мощность, работа и потери КПД электрических цепей |
| Синусоидальный ток и его основные параметры |
| Способы представления синусоидального тока |
| Резисторное сопротивление в цепи синусоидального тока |
| Конденсатор в цепи синусоидального тока |
| Индуктивность в электрической цепи |
| Закон электромагнитной индукции |
| Индуктивность в цепи синусоидального тока |
| Взаимоиндуктивность в магнитосвязанных цепях |
| Законы Кирхгофа для цепей синусоидального тока |
| Закон Ома и сопротивления цепи синусоидального тока с последовательным соединением элементов R, L,C |
| Понятие о резонансе напряжений |
| Резонанс напряжений и его признаки |
| Закон Ома и проводимость цепи синусоидального тока с параллельным соединением ветвей R-L, L-C |
| Понятие о резонанс токов |
| Мгновенная мощь цепи синусоидального тока |
| Активная, реактивная и полная мощность цепей синусоидального тока |
| Коэффициент мощности и его экономическое значение |
| Получение трехфазной системы ЭДС и способы представления |
| Соединения обмоток трехфазных генераторов |
| Соединения приемников в трехфазных цепях |
| Мощность трехфазных цепей |
| Трансформаторы |
| Работа трансформаторов в различных режимах |
| Потери и КПД трансформаторов |
| Устройство, схемы и группы соединения обмоток трехфазных трансформаторов |
| Назначение, схема и работа автотрансформатора |
| Назначение, схема и работа импульсного трансформатора |
| Машины постоянного тока |
| Асинхронные электродвигатели |
| Синхронные электродвигатели |
| Пускорегулирующая аппаратура |
| Выбор типа и мощности электродвигателя |
| Провода и кабели, выбор сечения проводов |
| Защитное заземление |
| Электронно-дырочный переход |
| Диоды, тиристоры |
| Транзисторы |
| Основные логические операции и их реализация |
| Триггеры |
| Однофазные неуправляемые выпрямители |
| Трехфазные выпрямители: нулевой, мостовой |
| Фильтры(C, L, LC, RC), коэффициент пульсаций |
| Однофазные и трехфазные управляемые выпрямители |
| All Pages |
Page 20 of 49
Понятие о резонанс токов. Условия его возникновения и способы осуществления
Резонанс токов — резонанс, происходящий в параллельном колебательном контуре при его подключении к источнику напряжения, частота которого совпадает с собственной частотой контура.
Условие резонанса токов: , .
В1 – реактивная проводимость первой ветви,
В2 – реактивная проводимость второй ветви.
Способ возбуждения колебаний в электрическом контуре, заключающийся в генерации колебаний, за счет регулирования сигнала, управляющего возбуждением колебаний.
Резонанс токов и его признаки
Режим, при котором в цепи, содержащей параллельные ветви с индуктивными и емкостными элементами, ток неразветвленного участка цепи совпадает по фазе с напряжением (φ=0), называют резонансом токов.
Признаки резонанса токов:
Реактивные составляющие токов ветвей равны IPC = IPL и находятся в противофазе в случае, когда напряжение на входе чисто активное;
Токи ветвей превышают общий ток цепи, который имеет минимальное значение и совпадают по фазе.
Last Updated on Sunday, 24 January 2016 04:34
Резонанс токов
Резонанс токов наблюдается в цепях, где индуктивность и емкость соединены параллельно.
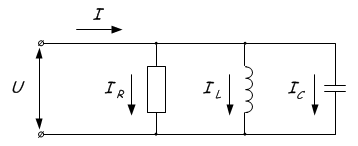
Явление заключается в протекании токов большой величины между конденсатором и катушкой, при нулевом токе в неразветвленной части цепи. Это объясняется тем, что при достижении резонансной частоты общее сопротивление Z возрастает. Или простым языком звучит так – в точке резонанса достигается максимальное общее значение сопротивления Z, после чего одно из сопротивлений увеличивается, а другое снижается в зависимости от того растет или снижается частота. Это наглядно отображено на графике:
В общем, всё аналогично предыдущему явлению, условия возникновения резонанса токов следующие:
- Частота питания аналогична резонансной у контура.
- Проводимости у индуктивности и ёмкости по переменному току равны BL=Bc, B=1/X.
Емкость и индуктивность в цепи переменного тока
Если в цепях постоянного тока емкость в общем смысле представляет собой разорванный участок цепи, а индуктивность — проводник, то в переменном конденсаторы и катушки представляют собой реактивный аналог резистора.
Реактивное сопротивление катушки индуктивности определяется по формуле:
Векторная диаграмма:
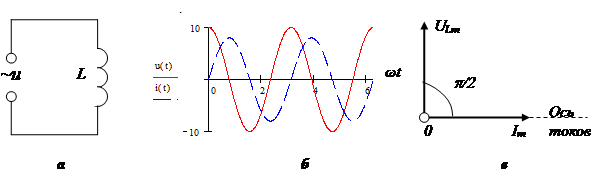
Реактивное сопротивление конденсатора:
Здесь w — угловая частота, f — частота в цепи синусоидального тока, L — индуктивность, C — емкость.
Векторная диаграмма:
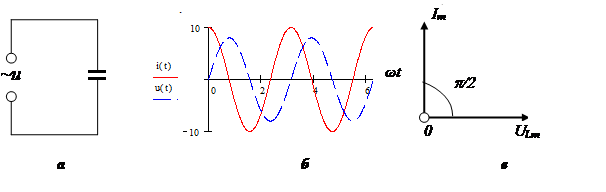
Стоит отметить, что при расчете соединенных последовательно реактивных элементов используют формулу:
Обратите внимание, что емкостная составляющая принимается со знаком минус. Если в цепи присутствует еще и активная составляющая (резистор), то складывают по формуле теоремы Пифагора (исходя из векторной диаграммы):. От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока
От чего зависит реактивное сопротивление? Реактивные характеристики зависят от величины емкости или индуктивности, а также от частоты переменного тока.
Если посмотреть на формулу реактивной составляющей, то можно заметить, что при определенных значениях емкостной или индуктивной составляющей их разность будет равна нулю, тогда в цепи останется только активное сопротивление. Но это не все особенности такой ситуации.
Применение на практике
Рассмотрим, какая польза и вред резонанса токов и напряжений. Наибольшую пользу явления резонанса принесли в радиопередающей аппаратуре. Простыми словами, а схеме приемника установлены катушка и конденсатор, подключенные к антенне. С помощью изменения индуктивности (например, перемещая сердечник) или величины емкости (например, воздушным переменным конденсатором) вы настраиваете резонансную частоту. В результате чего напряжение на катушке повышается и приемник ловит определенную радиоволну.

Вред эти явления могут на нести в электротехнике, например, на кабельных линиях. Кабель представляет собой распределенную по длине индуктивность и емкость, если на длинную линию подать напряжение в режиме холостого хода (когда на противоположном от источника питания конце кабеля нагрузка не подключена). Поэтому есть опасность того, что произойдет пробой изоляции, во избежание этого подключается нагрузочный балласт. Также аналогичная ситуация может привести к выходу из строя электронных компонентов, измерительных приборов и другого электрооборудования – это опасные последствия возникновения этого явления.
Применение резонансного явления
Резонанс в электрических цепях используют для фильтрации сигналов. Выбирают соответствующую схему обработки для ограничения необходимого диапазона либо расширения полосы пропускания.
С помощью последовательного контура можно повысить напряжение питания, если снабжающая организация не обеспечивает стабильность параметров сети. Такие неприятности встречаются при подключении потребителей на дачных участках и в коттеджных поселках, в сравнительно небольших населенных пунктах.
Недостаток ликвидируют конденсаторами, которые добавляют в электрическую цепь. Подобные решения помогают восстановить работоспособность дрели, станка, другого мощного оборудования. Обмотки соответствующего привода выполняют функции индуктивного компонента колебательного контура.
Параллельное подключение конденсаторов компенсирует потери, созданные реактивной мощностью. Этот вариант обеспечивает циркуляцию энергии между накопителем и подключенной обмоткой. Без такого дополнения часть энергии будет бесполезно потребляться сетью питания. Следует подчеркнуть, что счетчик в любом случае фиксирует потребление. Данная модернизация поможет сэкономить на оплате коммунальных услуг.
Резонансные явления способны чрезмерно увеличить силу тока или напряжение. Необходим точный расчет электрических цепей, чтобы предотвратить перегрев и повреждение проводов, короткие замыкания и другие аварийные ситуации.
Определение резонанса
Итак, в переводе с латыни слово «резонанс» буквально означает «откликаюсь», и означает физическое явление, при котором собственные колебательные движения, становясь вынужденными, многократно увеличивают свою амплитуду, отвечая на воздействия внешней среды.
Или если по-простому, то резонанс это отклик на некий раздражитель извне, это синхронизация частот колебаний (количества колебаний в секунду) определенного тела (или целой системы) с внешней силой, которая воздействует на него. Вследствие физического резонанса всегда происходит увеличение амплитуды колебаний тела или системы.
Впрочем, есть у резонанса и свой антипод – диссонанс. Диссонанс (с латыни переводится как «разногласящий») – прямо противоположное явление, означающее несовпадение, несоответствие. Если к тем же раскаченным качелям начать прикладывать силу хаотически, то есть хаотически их дергать туда-сюда, то вскоре они остановятся, амплитуда их движения снизится до нуля.






