Закон Кулона. Точечный заряд.
Силы электростатического взаимодействия зависят от формы и размеров наэлектризованных тел, а также от характера распределения заряда на этих телах. В некоторых случаях можно пренебречь формой и размерами заряженных тел и считать, что каждый заряд сосредоточен в одной точке.
Точечный заряд – это электрический заряд, когда размер тела, на котором этот заряд сосредоточен, намного меньше расстояния между заряженными телами. Приближённо точечные заряды можно получить на опыте, заряжая, например, достаточно маленькие шарики.
Взаимодействие двух покоящихся точечных зарядов определяет основной закон электростатики – закон Кулона. Этот закон экспериментально установил в 1785 году французский физик Шарль Огюстен Кулон (1736 – 1806). Формулировка закона Кулона следующая:
Эта сила взаимодействия называется кулоновская сила, и формула закона Кулона будет следующая:
F = k · (|q1| · |q2|) / r2
где |q1|, |q2| – модули зарядов, r – расстояния между зарядами, k – коэффициент пропорциональности.
Коэффициент k в СИ принято записывать в форме:
k = 1 / (4πε0ε)
где ε0 = 8,85 * 10-12 Кл/Н*м2 – электрическая постоянная, ε – диэлектрическая проницаемость среды.
Для вакуума ε = 1, k = 9 * 109 Н*м/Кл2.
Сила взаимодействия неподвижных точечных зарядов в вакууме:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2]
Если два точечных заряда помещены в диэлектрик и расстояние от этих зарядов до границ диэлектрика значительно больше расстояния между зарядами, то сила взаимодействия между ними равна:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2] = k · (1 /π) · [(|q1| · |q2|) / r2]
Диэлектрическая проницаемость среды всегда больше единицы (π > 1), поэтому сила, с которой взаимодействуют заряды в диэлектрике, меньше силы взаимодействия их на том же расстоянии в вакууме.
Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела (рис. 1.8).
Рис. 1.8. Силы взаимодействия двух неподвижных точечных заряженных тел.
Кулоновские силы, как и гравитационные силы, подчиняются третьему закону Ньютона:
F1,2 = -F2,1
Кулоновская сила является центральной силой. Как показывает опыт, одноимённые заряженные тела отталкиваются, разноимённо заряженные тела притягиваются.
Вектор силы F2,1, действующей со стороны второго заряда на первый, направлен в сторону второго заряда, если заряды разных знаков, и в противоположную, если заряды одного знака (рис. 1.9).
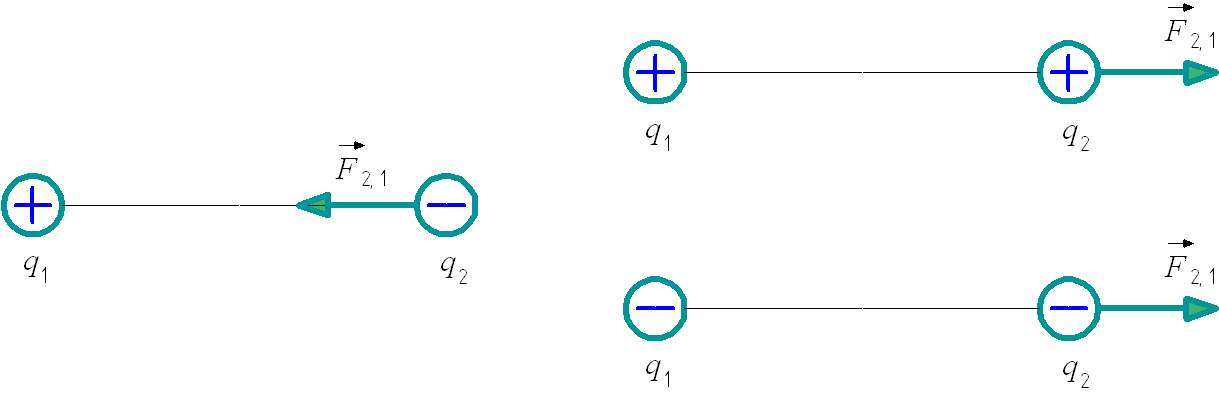
Рис. 1.9. Взаимодействие разноименных и одноименных электрических зарядов.
Электростатические силы отталкивания принято считать положительными, силы притяжения – отрицательными. Знаки сил взаимодействия соответствуют закону Кулона: произведение одноимённых зарядов является положительным числом, и сила отталкивания имеет положительный знак. Произведение разноимённых зарядов является отрицательным числом, что соответствует знаку силы притяжения.
В опытах Кулона измерялись силы взаимодействия заряженных шаров, для чего применялись крутильные весы (рис. 1.10). На тонкой серебряной нити подвешена лёгкая стеклянная палочка с
, на одном конце которой закреплён металлический шарика , а на другом противовесd . Верхний конец нити закреплён на вращающейся головке приборае , угол поворота которой можно точно отсчитывать. Внутри прибора имеется такого же размера металлический шарикb , неподвижно закреплённый на крышке весов. Все части прибора помещены в стеклянный цилиндр, на поверхности которого нанесена шкала, позволяющая определить расстояние между шарикамиa иb при различных их положениях.
Рис. 1.10. Опыт Кулона (крутильные весы).
При сообщении шарикам одноимённых зарядов они отталкиваются друг от друга. При этом упругую нить закручивают на некоторый угол, чтобы удержать шарики на фиксированном расстоянии. По углу закручивания нити и определяют силу взаимодействия шариков в зависимости от расстояния между ними. Зависимость силы взаимодействия от величины зарядов можно установить так: сообщить каждому из шариков некоторый заряд, установить их на определённом расстоянии и измерить угол закручивания нити. Затем надо коснуться одного из шариков таким же по величине заряженным шариком, изменяя при этом его заряд, так как при соприкосновении равных по величине тел заряд распределяется между ними поровну. Для сохранения между шариками прежнего расстояния необходимо изменить угол закручивания нити, а следовательно, и определить новое значение силы взаимодействия при новом заряде.
Применение на практике
Работы Кулона очень важны в электростатике, на практике они применяется в целом ряде изобретений и устройств. Ярким примером можно выделить молниеотвод. С его помощью защищают здания и электроустановки от грозы, предотвращая тем самым пожар и выход из строя оборудования. Когда идёт дождь с грозой на земле появляется индуцированный заряд большой величины, они притягиваются в сторону облака. Получается так, что на поверхности земли появляется большое электрическое поле. Возле острия молниеотвода оно имеет большую величину, в результате этого от острия зажигается коронный разряд (от земли, через молниеотвод к облаку). Заряд от земли притягивается к противоположному заряду облака, согласно закону Кулона. Воздух ионизируется, а напряженность электрического поля уменьшается вблизи конца молниеотвода. Таким образом, заряды не накапливаются на здании, в таком случае вероятность удара молнии мала. Если же удар в здание и произойдет, то через молниеотвод вся энергия уйдет в землю.
В серьезных научных исследованиях применяют величайшее сооружение 21 века – ускоритель частиц. В нём электрическое поле выполняет работу по увеличению энергии частицы. Рассматривая эти процессы с точки зрения воздействия на точечный заряд группой зарядов, тогда все соотношения закона оказываются справедливыми.
Напоследок рекомендуем просмотреть видео, на котором предоставлено подробное объяснение Закона Кулона:
Полезное по теме:
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов. Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
.
где |q1| и |q2| — модули зарядов; r — расстояние между ними; k — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока — 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока 1 А за 1 с.
Заряд в 1 Кл очень велик. Сила взаимодействия двух точечных зарядов по 1 Кл каждый, расположенных на расстоянии 1 км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой 1 т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в 1 А — вполне обычный ток, протекающий по проводам в наших квартирах).
Коэффициент k в законе Кулона при его записи в СИ выражается в Н · м 2 /Кл 2 . Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:
k = 9 · 10 9 Н·м 2 /Кл 2 .
Часто его записывают в виде , где ɛ =8,85 · 10 — 12 Kл 2 H·м 2 — электрическая постоянная. В среде с диэлектрической проницаемостью ɛ закон Кулона имеет вид:
.
Дивергенция и ротор (Как вы это поняли).
На рис.6.7 представлены различные картины векторного поля. Попробуйте сказать,
где ротор и дивергенция равны 0, а где нет
При этом прежде всего нужно обратить
внимание на контуры интегрирования, заметив, что они выбраны так, чтобы вдоль
каждой из сторон, проекция векторов поля имела одно и тоже значение (причём
для двух сторон в случаях а, б, г, д она равна 0)
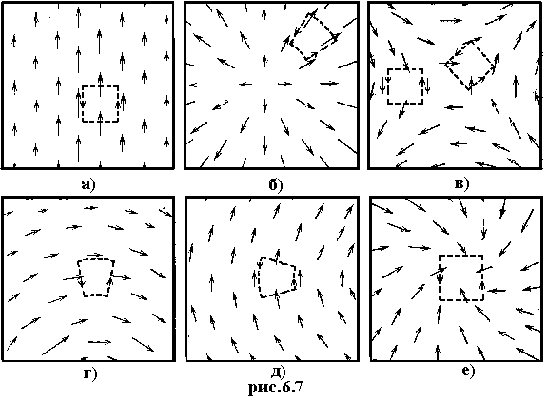
|
вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. ротор не равен нулю. Сравните с рекой. |
Явно виден источник поля. Дивергенция не равна нулю. Поле центрально — симметричное. Поэтому ротор равен 0. |
вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Проекции векторов поля на противоположные стороны контура разных знаков, но одинаковы по абсолютной величине, и поэтому при сложении линейных интегралов они уничтожают друг друга. Поэтому ротор равен нулю. |
|
вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор убывает по мере удаления от центра поля (за пределами рисунка) поэтому ротор может быть равен 0. |
вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор не убывает, поэтому линейный интеграл по левой стороне контура не компенсируется таким же интегралом по правой. Поэтому ротор не равен нулю. |
Явно виден сток поля. Поэтому дивергенция не равна 0. Так же и ротор не равен нулю, поскольку циркуляция вдоль указанного контура не равна 0, так как проекции векторов поля на все стороны контура одного знака (отрицательны) и при сложении (интегрировании) не компенсируют друг друга. |
Подводя итог, ещё раз отметим, что ротор характеризует степень
завихрённости векторного поля, его «вращательную составляющую». При этом, однако,
нужно иметь в виду, что данная «вращательная компонента» поля может быть обусловлена
не только искривлением векторных линий (завихрённость «в чистом виде»), как
при вытекании воды из ванны, или в примере е), но и поперечной неоднородностью
поля, когда векторные линии — прямые, как в случае течения воды в реке (рис.6.5),
или в случае примера а).
Электрические заряды. Точечный заряд. Закон Кулона
Электрический заряд — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году.
Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с. Заряд в один кулон очень велик. Если бы два носителя заряда (q1 = q2 = 1 Кл) расположили в вакууме на расстоянии 1 м, то они взаимодействовали бы с силой 9·109 H, т.е. с силой, с которой гравитация Земли притягивала бы предмет с массой порядка 1 миллиона тонн.
Электрический заряд любой системы тел состоит из целого числа элементарных зарядов, равных примерно 1,6 · 10−19 Кл в системе СИ или 4,8 · 10−10 ед. СГСЭ. Носителями электрического заряда являются электрически заряженные элементарные частицы. Наименьшей по массе устойчивой в свободном состоянии частицей, имеющей один отрицательный элементарный электрический заряд, является электрон (его масса равна 9,11·10−31 кг).
Электрический заряд замкнутой системы сохраняется во времени и квантуется — изменяется порциями, кратными элементарному электрическому заряду, то есть, другими словами, алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе.
Точечный заряд — идеализация, вводимая для упрощения описания поля заряженного тела или системы тел. Иногда также определяется как электрически заряженнаяматериальная точка.
Более простыми словами, точечный заряд — заряд, размерами носителя которого по сравнению с расстоянием, на котором рассматривается электростатическое взаимодействие, можно пренебречь.
Именно для точечных зарядов сформулирован закон Кулона.
Закон Кулона — это закон, описывающий силы взаимодействия между точечными электрическими зарядами.
Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:
Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.
Важно отметить, что для того, чтобы закон был верен, необходимы:
— точечность зарядов — то есть расстояние между заряженными телами много больше их размеров — впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;
— их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;
— взаимодействие в вакууме.
В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:
где — сила, с которой заряд 1 действует на заряд 2; — величина зарядов; — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами — ); — коэффициент пропорциональности. Таким образом, закон указывает, что одноимённые заряды отталкиваются (а разноимённые — притягиваются).
В Международной системе единиц (СИ) одной из основных единиц является единица силы электрического тока ампер, а единица заряда — кулон — производная от него. Величина ампера определена таким образом, что k = c2 · 10-7 Гн/м = 8,9875517873681764 · 109 Н · м2/Кл2 (или Ф−1 · м).
В СИ коэффициент k записывается в виде:
где ≈ 8,854187817 · 10−12 Ф/м — электрическая постоянная.
Понятие электрического поля.
Теперь несколько замечаний об электрическом поле. На вопрос о том, что такое
электрическое поле, реально ли оно или это некий числовой коэффициент, ответить
очень трудно. “Есть вещи, которые вы спокойно можете объяснить два раза, не
рискуя, что кто-нибудь поймет, о чем вы говорите”, — считала Сова в сказке о
Винни-Пухе. К понятию поля мы будем возвращаться неоднократно. Пока речь идет
об электростатическом поле. А ведь есть еще магнитное и электрическое вихревое,
и даже электромагнитное.
Понятие “электрическое поле” имеет смысл. Оно сообщает пространству локальное
свойство, а именно: если нам известно значение поля, то мы знаем без дальнейших
рассуждений, что случится с любыми зарядами в этой точке, и для этого нам совсем
не нужно знать, как это поле было создано. Напряженность — это количественная
характеристика поля.
Физика для средней школы
Точечный и распределенный заряды
Идеальной физической моделью заряда в электростатике является точечный заряд.
Точечным зарядом называется заряд, сосредоточенный на теле, размерами которого можно пренебречь по сравнению с расстоянием до других тел или до рассматриваемой точки поля. Иными словами, точечный заряд — это материальная точка, которая имеет электрический заряд.
Если заряженное тело настолько велико, что его нельзя рассматривать как точечный заряд, то в этом случае необходимо знать распределение зарядов внутри тела.
Выделим внутри заряженного тела малый объем и обозначим через электрический заряд, находящийся в этом объеме. Предел отношения , когда объем неограниченно уменьшается, называют объемной плотностью электрического заряда в данной точке. Обозначают ее буквой :
Единицей объемной плотности заряда в СИ является кулон на кубический метр (Кл/м3).
В случае неравномерно заряженного тела плотность различна в разных точках. Распределение заряда в объеме тела задано, если известно как функция координат.
В металлических телах заряды распределяются только внутри тонкого слоя, прилегающего к поверхности. В этом случае удобно пользоваться поверхностной плотностью заряда , которая представляет собой предел отношения заряда к площади поверхности, по которой распределен этот заряд:
где — заряд, находящийся на участке поверхности площадью .
Следовательно, поверхностная плотность заряда измеряется зарядом, приходящимся на единицу поверхности тела. Распределение зарядов по поверхности описывается зависимостью поверхностной плотности (x, y, z) от координат точек поверхности.
Единицей поверхностной плотности заряда в СИ является кулон на квадратный метр (Кл/м2).
В том случае, если заряженное тело по форме представляет собой нить (диаметр поперечного сечения тела много меньше его длины , удобно использовать линейную плотность заряда
где — заряд, находящийся на длине тела.
Единицей линейной плотности заряда в СИ является кулон на метр (Кл/м).
Если известно распределение зарядов внутри тела, то можно вычислить напряженность электростатического поля, создаваемого этим телом. Для этого заряженное тело мысленно разбивают на бесконечно малые части и, рассматривая их как точечные заряды, вычисляют напряженность поля, создаваемую отдельными частями тела. Суммарную напряженность поля находят затем суммированием полей, создаваемых отдельными частями тела, т.е.
Потенциал электрического поля. Разность потенциалов
Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.
Обозначение – \( \varphi \), единица измерения в СИ – вольт (В).
Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.
Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:
Обозначение – \( \Delta\varphi \), единица измерения в СИ – вольт (В).
Иногда разность потенциалов обозначают буквой \( U \) и называют напряжением.
Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:. Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле
В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки
Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле. В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность
В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность
В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал поля точечного заряда \( q \) в точке, удаленной от него на расстояние \( r \), вычисляется по формуле:
Для наглядного представления электрического поля используют эквипотенциальные поверхности.
Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (\( r =R \), где \( R \) – радиус шара). Напряженность поля внутри шара равна нулю. Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение
Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.
Свойства эквипотенциальных поверхностей
- Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
- Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.
Разность потенциалов и напряженность связаны формулой:
Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:
Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.
Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил. Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил
Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.
Алгоритм решения таких задач:
- установить характер и особенности электростатических взаимодействий объектов системы;
- ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
- записать законы сохранения и движения для объектов;
- выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
- составить систему уравнений и решить ее относительно искомой величины;
- проверить решение.
Напряженность электрического поля
Электрические поля проявляются в силовом взаимодействии между зарядами. Сила взаимодействия между зарядами $q$ и $q_1$ находится с помощью закона Кулона:
$$F=k{qq_1\over r^2}$$
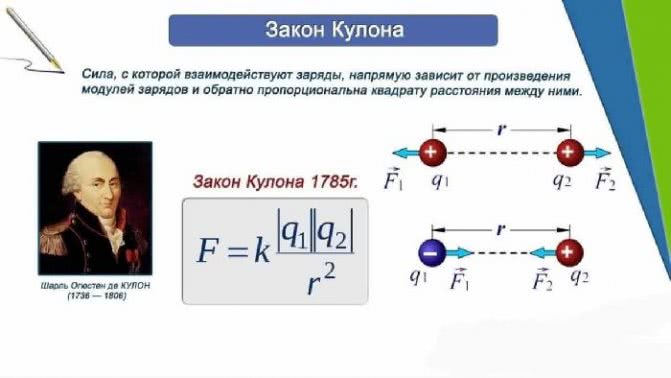
Рис. 1. Закон Кулона.
Если рассмотреть поле, порождаемое зарядом $q$, то при фиксированном заряде $q_1$ и расстоянии $r$, сила взаимодействия между зарядами будет прямо пропорциональна величине заряда $q$. А значит, отношение этой силы к заряду $q$ не зависит от $q$, и может быть принято, как силовая характеристика поля.
Напряженность электрического поля — это отношение силы, действующей на пробный заряд, помещаемый в поле, к величине этого заряда.
$$\overrightarrow E={\overrightarrow F \over q}$$
Напряженность поля — векторная величина, имеющая то же направление, что и направление силы, действующей на положительный заряд.
Если в каждой точке поля изобразить вектор напряженности, то эти векторы сольются в линии, которые называются линиями напряженности. Они полностью характеризуют распределение поля в пространстве. На пробный положительный заряд, помещенный в поле, будет действовать сила, касательная к линии напряженности, проходящей через эту точку.
Например, так выглядит поле двух разноименных зарядов, находящихся рядом:

Рис. 2. Лини напряженности диполя.






