Закон Ома для электрической цепи
В основе расчёта входного и выходного напряжения цепи лежит закон Ома, знакомый ещё со школы по курсу физики. Базовая формула расчёта напряжения на участке цепи выглядит так:

Определить напряжение в цепи переменного тока можно по следующей формуле:
в этой формуле Z означает сопротивление (Ом), которое было получено на протяжении всей цепи.
В ряде случаев показатели не могут быть рассчитаны по этим фармулам напрямую.
- В случаях нахождения проводников или диэлектриков под воздействием высокого напряжения.
- В случаях быстро изменяющихся электромагнитных полей при прохождении токов высокой частоты. В этом случае требуется учитывать также инерцию переносящих заряд частиц.
- В условиях возникновении свойств сверхпроводимости, если цепи работают при экстремально низких температурах.
- При нагреве проводника протекающим по нему током.
- Для светодиодов. Зависимость между током и падением напряжения в этом случае нелинейная.
- Для процессов в устройствах на основе полупроводников.
В зависимости от того, как элементы включены в цепь – последовательно или параллельно – общее сопротивление рассчитывают по-разному.
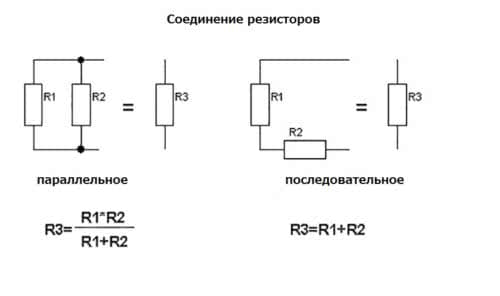
Расчёт при последовательном подключении
При последовательном соединении элементы идут друг за другом, и выход предыдущего соединяется с входом последующего. Общее сопротивление в этом случае можно посчитать по формуле:
Как определить и подобрать мощность
Данный параметр избирается от максимального значения силы заряженных частиц, которые будут протекать через проводник.
Для того чтобы подбирать тепловое рассеивание участков сопротивления для конкретных электроприборов, необходимо изучить параметры входного и выходного напряжения, а также силу электроцепи.
Далее будет представлен стандартный ряд с графическим изображением мощностного отбора резистантов. Абсолютное большинство фабричных электроприборов оснащаются схемами, где указан конкретный диапазон элементов. Такие схемы незаменимы при ремонте и позволяют быстро подбирать необходимое.
Стандартный ряд мощностей и их обозначение на схемах
| Вт | Условное обозначение на электросхемах |
| 0,05 Вт | |
| 0,125 Вт | |
| 0,025 Вт | |
| 0,5 Вт | |
| 1 Вт | |
| 2 Вт | |
| 5 Вт |
В качестве графических обозначений используются римские цифры и черточки, раскрывающие диапазон от 0,05 до 25
Информация о напряжении
Напряжение — работа электрического тока, при которой происходит перемещение заряда из одной точки в другую. Оно имеет векторное направление. Электрическим током является движение заряженных элементарных частиц под воздействие электромагнитного поля.
Некоторые начинающие физики не знают, в чем измеряется напряжение
Знать это очень важно, поскольку элементы электрической цепи можно рассчитать неверно. Единицей измерения тока является ампер (А), а напряжения — вольт (В). В последнем случае применяется вольтметр — прибор, измеряющий величину напряжения или разности потенциалов
Он подключается параллельно в систему. Например, нужно измерить его значение на лампочке накаливания. Для этого необходимо подключиться параллельно к ней, а не последовательно
В последнем случае применяется вольтметр — прибор, измеряющий величину напряжения или разности потенциалов. Он подключается параллельно в систему. Например, нужно измерить его значение на лампочке накаливания. Для этого необходимо подключиться параллельно к ней, а не последовательно.
Физический смысл
Под физическим смыслом напряжения или разности потенциалов понимают работу, необходимую для перемещения точечного заряда в 1 Кл из одного места в другое. В этом случае переносится только положительный потенциал. При этом возникает электродвижущая сила (ЭДС), которая называется напряжением или разностью потенциалов.
Для понимания физического смысла следует рассмотреть более простой пример. Пусть существует некоторая система, состоящая из насоса, труб и крана. Насос — напряженность электрического поля, трубы — провода, а кран — сопротивление системы. При включении первого происходит закачивание воды. Если немного приоткрыть кран, то она польется маленькой струйкой. При открытии его полностью жидкость будет уходить более интенсивно.
Формулы для вычислений
Все формулы для расчетов построены на законах Ома. Их всего два: для участка и для всей цепи. Формулировка первого: ток, протекающий на искомом участке, прямо пропорционален U и обратно пропорционален R. Его математическая запись имеет такой вид: I=U/R. Из последнего получаются такие соотношения:
- U=IR.
- R=U/I.
- P=IU=(I2 )R=(U2 )/R, где Р — мощность.
Для полной цепи закон формулируется иначе: ток I прямо пропорционален ЭДС (E) и обратно пропорционален алгебраической сумме внешнего R и внутреннего r сопротивлений. Следует отметить, что r — проводимость источника питания. Записывается он в таком виде: I=E/(R+r). Физики вывели следующие соотношения, помогающие при расчетах:
- Е=I (R+r).
- R=(E/I)-r.
- r=(E/I)-R.
- Р=ЕI=(E2 )/(R+r)=(R+r)I2.
Тождества для переменного тока
Напряжение при переменном токе классифицируется на определенные виды. К ним относятся следующие:
- Мгновенное или действующее — параметр, который измеряют приборы (Um).
- Амплитудное — величина, характеризующее максимальную величину в определенный момент времени. Расчитывается по формуле с учетом угловой частоты (w), времени (t) и угла между фазами (f), который измеряется осциллографом: u (t)=Uмsin (wt+f).
- Среднеквадратичное (Uq) — величина, вычисляемая по формуле: Uq=0,7073Uм).
Для расчета следует иметь знания об индуктивной Xl, емкостной Xc и резистивной R нагрузках. Первая — проводимость всех элементов, содержащих индуктивность (катушки, трансформаторы, электродвигатели). Во втором случае учитываются все емкостные радиодетали (варисторы и конденсаторы). Резистивная нагрузка включает все значения резисторов.
Полный импеданс цепи (Z) равен сумме всех элементов, содержащий активную, индуктивную и емкостную. Специалисты рекомендуют использовать такие формулы, необходимые для расчетов:
- Xl=wL.
- Хс=1/wC.
- Z=R+Xc+Xl.
- I=Uм/Z.
- Uм=IZ.
- Z=Uм/I.
Четвертая формула является законом Ома для участка цепи, которую следует применять при переменных токах.
Таким образом, при помощи формулы напряжения можно рассчитывать не только основные параметры электричества для постоянного и переменного токов, но и его допустимые величины для человека.
Закон Ома для всей цепи.ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Вольтметр, подключенный к лампочке, показывает U = 4 В, а амперметр — I = 2 А (рис. 6-10). Чему равно внутреннее сопротивление r источника тока, к которому эта лампочка присоединена, если ЭДС источника ε = 5 В?Примечание: если в условии задачи ничего не сказано о сопротивлении амперметра, то этим сопротивлением можно пренебречь, а если ничего не сказано о сопротивлении вольтметра, то его следует считать бесконечно большим, а силу тока, текущего через вольтметр, равной нулю.
РЕШЕНИЕ.
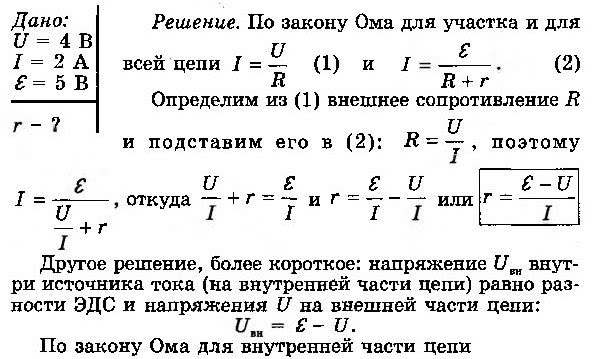
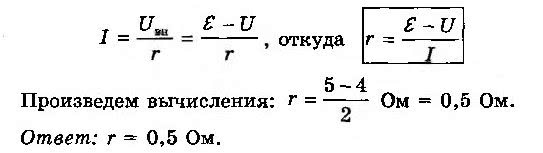
Задача № 2.
Дана схема (рис. 6-11, а). Во сколько раз изменится сила тока, текущего в неразветвленной части цепи, и напряжение на полюсах источника тока, если ключ К замкнуть? Сопротивление лампы Л2 вдвое больше сопротивления лампы Л1, а внутреннее сопротивление источника тока в 10 раз меньше сопротивления лампы Л1. 
Задача № 3.
В резисторе сопротивлением R = 5 Ом сила тока I = 0,2 А. Резистор присоединен к источнику тока с ЭДС ε = 2 В. Найти силу тока короткого замыкания Iк.з.
Задача № 4.
Вольтметр, подключенный к полюсам источника тока при разомкнутой внешней цепи, показал U1 = 8 В. Когда же цепь замкнули на некоторый резистор (рис. 6-12, а), вольтметр показал U2 = 5 В. Что покажет этот вольтметр, если последовательно к этому резистору подключить еще один такой же (рис. 6-12, б) ? Что покажет этот вольтметр, если второй резистор присоединить к первому параллельно (рис. 6-12, в)? 
Задача № 5.
Цепь питается от источника тока с ЭДС ε = 4 В и внутреннем сопротивлением г = 0,2 Ом. Построить график зависимости силы тока I в цепи и напряжения U на полюсах источника тока от внешнего сопротивления R.
Задача № 6.
Амперметр, будучи накоротко присоединен к гальваническому элементу с ЭДС ε = 2 В и внутренним сопротивлением r = 0,2 Ом, показал ток силой I1 = 3 А . Какую силу тока I2 покажет этот амперметр, если его зашунтировать сопротивлением Rш = 0,1 Ом?
Задача № 7.
Дана схема (рис. 6-16). Емкости конденсаторов С1, С2 и ЭДС источника тока ε известны. Известно также, что ток короткого замыкания Iк.з. этого источника в три раза превосходит ток I, текущий в этой цепи. Найти напряженности Е1 и Е2 полей в конденсаторах, если расстояния между их обкладками равны d.
Задача № 8.
Дана схема (рис. 6-17). Известны емкости С и 2С конденсаторов, сопротивления R и 2R проводников и ЭДС источника тока ε. Внутренним сопротивлением источника тока можно пренебречь (г = 0). Определить напряжения U1 и U2 на конденсаторах и заряды q1 и q2 этих конденсаторов. 
Задача № 9.
Имеется N одинаковых источников тока, которые соединяют сначала последовательно, затем параллельно, подключая каждый раз к одному и тому же внешнему сопротивлению R. Внутреннее сопротивление каждого источника r. Во сколько раз при этом изменяется напряжение на внешней части цепи?
Задача № 10.
Электрическая цепь состоит из источника тока с ЭДС ε = 180 В и потенциометра сопротивлением R = 5 кОм. Ползунок потенциометра стоит посередине прибора (рис. 6-21, а). Найти показания вольтметров U1 и U2, подключенных к потенциометру, если их сопротивления R1= 6 кОм и R2 = 4 кОм. Внутренним сопротивлением r источника тока пренебречь. 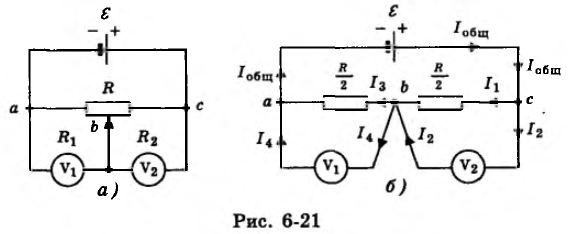
Задача № 11.
Дана схема, изображенная на рис. 6-22, а. Сопротивления R1, R2 и R известны. Известны также ЭДС источника тока ε и его внутреннее сопротивление r. Найти силу тока I2 в сопротивлении R2. 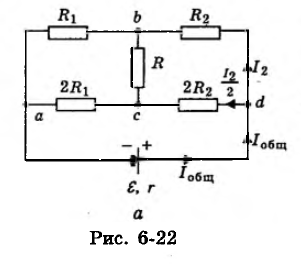
Задача № 12.
Проволока из нихрома образует кольцо диаметром D = 2 м (рис. 6-23, а). В центре кольца помещен источник тока с ε = 2В и внутренним сопротивлением r = 1,5 Ом, соединенный в точках а и b с кольцом такой же проволокой. Найти разность потенциалов φb – φа между точками b и а. Удельное сопротивление нихрома р = 1,1 мкОм•м, площадь поперечного сечения проволоки S = 1 мм2. 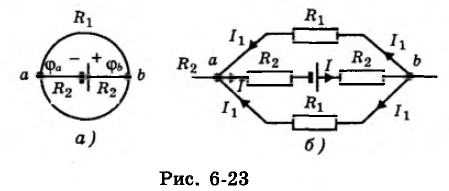
Это конспект по теме «Закон Ома для всей цепи. ЗАДАЧИ на ЕГЭ». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Маркировка переменных резисторов
Российская маркировка переменных сопротивлений до 1980 года – например, СП4-18:
- Тип изделия обозначается СП.
- Первая цифра – разновидность материала и технология изготовления – 4.
- Вторая – регистрационный номер типа резистора –18.
Маркировка группы по технологии изготовления и материалу:
- 1 – непроволочные тонкослойные углеродистые и бороуглеродистые;
- 2 – непроволочные тонкослойные металлопленочные и металлооксидные;
- 3 – непроволочные композиционные пленочные;
- 4 – непроволочные композиционные объемные;
- 5 – проволочные;
- 6 – непроволочные тонкослойные металлизированные.
Сейчас действует новая система маркировки переменных и подстроечных резисторов – например, РП1-46:
- Тип изделия обозначается РП.
- Первая цифра определяет группу по материалу резистивного элемента (1 – непроволочные, 2 – проволочные и металлофольговые).
- Вторая цифра – регистрационный номер разработки конкретного типа сопротивления.
Таблица номиналов
| 1 Ом | 10 Ом | 100 Ом | 1 кОм | 10 кОм | 100 кОм | 1 МОм | 10 МОм |
| 1.5 Ом | 15 Ом | 150 Ом | 1.5 кОм | 15 кОм | 150 кОм | 1.5 МОм | 15 МОм |
| 2.2 Ом | 22 Ом | 220 Ом | 2.2 кОм | 22 кОм | 220 кОм | 2.2 МОм | 22 МОм |
| 3.3 Ом | 33 Ом | 330 Ом | 3.3 кОм | 33 кОм | 330 кОм | 3.3 МОм | 33 МОм |
| 4.7 Ом | 47 Ом | 470 Ом | 4.7 кОм | 47 кОм | 470 кОм | 4.7 МОм | 47 МОм |
| 6.8 Ом | 68 Ом | 680 Ом | 6.8 кОм | 68 кОм | 680 кОм | 6.8 МОм | 68 МОм |
Схема делителя напряжения на резисторах
Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.
Тестер транзисторов / ESR-метр / генератор
Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…
Подробнее
Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Что такое делитель напряжения
Верхним плечомнижним плечом
Делители напряжения бывают на резисторах, на конденсаторах, на катушках индуктивности.
Делители напряжения на резисторах
Делители напряжения могут применяться как в цепях постоянного тока, так и в цепях тока переменного. Делители напряжения на резисторах подходят и для тех, и для других цепей, однако используются они только в цепях низкого напряжения. Для питания устройств делители напряжения на резисторах не применяют.
В простейшем виде резистивный делитель напряжения состоит всего из пары резисторов,
соединенных последовательно. Делимое напряжение подается на делитель, в результате на каждом резисторе падает определенная доля этого напряжения, пропорциональная номиналу резистора. Сумма падений напряжений равна здесь напряжению подаваемому на делитель.
Согласно закону Ома для участка электрической цепи, на каждом резисторе падение напряжения будет прямо пропорционально току и величине сопротивления резистора. А согласно первому правилу Кирхгофа, ток через данную цепь будет везде один и тот же
Так, на каждый резистор придутся падения напряжения:
И напряжение на концах участка цепи будет равно:
А ток в цепи делителя составит:
Теперь если подставить выражение для тока в формулы для падений напряжений на резисторах, то получим формулы для нахождения величин напряжений на каждом из резисторов делителя:
Используя делитель напряжения на резисторах для тех или иных целей, важно понимать, что присоединенная к одному из плеч делителя нагрузка, будь то измерительный прибор или что-нибудь другое, должна иметь собственное сопротивление значительно большее (в 10-100 раз), чем общее сопротивление резисторов, образующих делитель. Так, чтобы в расчетах этим сопротивлением, включенным параллельно R2, можно было бы пренебречь.Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму. Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке (см
выше, в предыдущем абзаце). Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R = R1+R2. Остается только взять конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко требуемому отношению напряжений, а сумма величин близка расчетной.
Расчёт делителя напряжения, состоящего из более чем трех резисторов можно по специальным формулам. Существуют методики, позволяющие выводить формулы для схем, содержащих от четырех и более резисторов.
Как понизить напряжение с помощью резистора
Чтобы нагрузка, которую требуется запитать, не сгорела, часто возникает необходимость снизить входное напряжение. Проще всего этого можно добиться, используя схему с двумя резисторами, более известную как делитель напряжения. Классическая схема выглядит так:
В этом случае напряжение подаётся на два резистора с использованием параллельного подключени, а на выходе его получают с одного. Подбор номиналов резисторов осуществляют по формуле так, чтобы напряжение, снимаемое на выходе, составляло какую-то часть от подаваемого. Расчет резистора для понижения напряжения можно воспользовавшись формулой, основанной на законе Ома:
Uвых= (Uвх*R2)/(R1+R2), где
Uвх – напряжение на входе, В;
Uвых – напряжение на выходе, В
R1 – показатель сопр. 1-ого резистора (Ом)
R2 – показатель сопр. 2-ого элемента, (Ом)
Подбор резистора для понижения напряжения
Для подбора нужного сопротивления резистора можно воспользоваться готовыми онлайн-калькуляторами или программами для моделирования работы электронных схем. Симуляторы электрических цепей способны не только рассчитать напряжение на выходе в зависимости от сопротивления элементов и способа их подключения, но и обладают функционалом, позволяющим визуализировать то, как падает ток и напряжение на резисторе. Например, приложение EveryCircuit позволяет изменять в схеме параметры элементов, выбирать скорость симуляции, получать данные в различных точках. При этом можно наблюдать за динамикой изменения значений, используя для ввода входных параметров вращающийся лимб в нижнем правом углу.
Существует ещё ряд бесплатных программ для эмуляции, позволяющие выполнить, в том числе, расчёт резистора при понижении напряжения, например:
- EasyEDA;
- Circuit Sims;
- DcAcLab;
и другие.
В статье мы ознакомились с понятием сопротивления, узнали о его единицах измерения, о маркировке резисторов, о программах эмулирующих работу цепи и облегчающих подбор нужного сопротивления, а также рассмотрели примеры расчёта падения напряжения на резисторе.
Что такое падение напряжения на резисторе
Электрический ток, проходя по цепи, испытывает сопротивление, которое может изменяться под воздействием разнообразных условий внешней среды (экстремально низкие температуры или нагрев) и может зависеть от характеристик конкретного проводника. Например, чем тоньше проводник или длиннее – тем оно выше.
На значение его величины влияют следующие факторы:
- сила тока;
- длина проводящих частей;
- напряжение;
- материал проводниковых элементов;
- нагрев (температура);
- площадь поперечного сечения.
Резисторы можно разделить на постоянные, переменные и подстроечные. Главное их отличие друг от друга – возможность изменения показателя сопротивления. Чаще всего встречаются постоянные резисторы – данный показатель в них нельзя изменить, поэтому они и получили такое название. Переменные отличаются тем, что величину сопротивления в них можно настраивать. В подстроечном резисторе её также можно изменять, но отличие данной разновидности в том, что он не рассчитан на частое изменение параметра. Подстроечные резисторы выполняются в более компактном корпусе по сравнению с переменными.
Чтобы вычислить падение напряжения на резисторе, нужно помнить, что снижение нагрузки, приложенной ко всей цепи (то есть, напряжения, подключённого к контуру) может быть получено как для всего контура, так и для любого элемента цепи. Напряжение понижается за счёт сопротивления, которым обладают проводники.
Падение напряжения на резисторе зависит от силы проходящего тока и характеристик проводников. Температура и показатели тока также имеют значение. Например, напряжение, измеренное вольтметром на лампочке, подключённой к сети 220 В, будет немного ниже за счёт сопротивления, которым обладает лампочка.
Источники питания имеют разную величину напряжения. Это значение может превышать то, которое бывает необходимо на выходе. Чтобы нагрузка, которую требуется запитать, не сгорела, часто возникает необходимость в понижении вольтажа, в том числе с помощью резисторов.
Сравнительная таблица напряжений
| Источник питания | Напряжение |
| NiCd аккумулятор | 1,2 В |
| Литий-железо-фосфатный аккумулятор | 3,3 В |
| Батарея типа «Крона» | 9 В |
| Автомобильный аккумулятор | 12 В |
| Аккумулятор для грузовых автомобилей | 24 В |
В этом случае резистор должен уменьшить протекающий по цепи ток. При этом ток не превращается в тепло, происходит именно его ограничение. То есть при включении резистора в цепь ток упадёт – в этом и состоит работа резистора, при совершении которой элемент нагревается.
В общем случае падения напряжения можно рассчитать, используя простую формулу, связывающее показатели между собой.
Но в ряде случаев, например, при параллельном подключении сопротивлений, посчитать необходимую величину уже сложнее. В этом случае по специальной формуле потребуется привести сопротивление параллельных веток к одному числу:
R = R1*R2 / (R1+R2)
При необходимости также учитываются другие сопротивления, суммирующиеся с этим значением (например, сопротивление провода и источника питания).
Материалы, из которых изготавливаются резисторы
В мире можно найти резисторы, изготовленные из самых разных материалов, каждый из которых имеет свои свойства и определенные области применения. Большинство инженеров-электронщиков используют типы, указанные ниже.
Проволочные резисторы
Рисунок 9 – Проволочные резисторы
Проволочные резисторы изготавливаются путем наматывания по спирали проволоки с высоким сопротивлением вокруг непроводящего сердечника. Обычно они применяются там, где нужна высокая точность или большая мощность. Сердечник обычно изготавливается из керамики или стекловолокна, а резистивная проволока из никель-хромового сплава, которая не подходит для приложений с частотами выше 50 кГц. Достоинствами проволочных резисторов являются низкий уровень шума и устойчивость к колебаниям температуры. Доступны резисторы со значениями сопротивления от 0,1 до 100 кОм и с точностью от 0,1% до 20%.
Металлопленочные резисторы
Рисунок 10 – Металлопленочные резисторы
Для металлопленочных резисторов обычно используют нитрид нихрома или тантала. Резистивный материал обычно составляет комбинация керамического материала и металла. Значение сопротивления изменяется путем вырезания с помощью лазера или абразива спирального рисунка в пленке, очень похожей на углеродную пленку. Металлопленочные резисторы обычно менее стабильны при изменениях температуры, чем проволочные резисторы, но лучше справляются с более высокими частотами.
Металлооксидные пленочные резисторы
Рисунок 11 – Металлооксидные пленочные резисторы
В металлооксидных резисторах используются оксиды металлов, такие как оксид олова, что немного отличает их от металлопленочных резисторов. Эти резисторы надежны и стабильны и работают при более высоких температурах, чем металлопленочные резисторы. По этой причине металлооксидные пленочные резисторы используются в приложениях, требующих высокой износостойкости.
Фольговые резисторы
Рисунок 12 – Фольговые резисторы
Фольговый резистор, разработанный в 1960-х годах, по-прежнему остается одним из самых точных и стабильных типов резисторов, которые вы найдете, и которые используются в приложениях с высокими требованиями к точности. Резистивный элемент составляет тонкая объемная металлическая фольга, которая приклеена на керамическую подложку. Фольговые резисторы имеют очень низкий температурный коэффициент сопротивления (ТКС).
Углеродные композиционные резисторы
Рисунок 13 – Углеродные композиционные резисторы
До 1960-х годов углеродные композиционные резисторы были стандартом для большинства приложений. Они надежны, но не очень точны (их допуск не может быть лучше примерно 5%). Для резистивного элемента углеродных резисторов используется смесь мелких частиц углерода и непроводящего керамического материала. Резистивному веществу придают форму цилиндра и запекают. Величину сопротивления определяют размеры корпуса и соотношение углерода и керамики. Использование большего количества углерода в процессе означает более низкое сопротивление. Углеродные композиционные резисторы по-прежнему полезны для определенных приложений из-за своей способности выдерживать мощные импульсы, хорошим примером применения может быть источник питания.
Углеродные пленочные резисторы
Углеродные пленочные резисторы представляют собой тонкую углеродную пленку (разрезанную по спирали для увеличения резистивного пути) на изолирующем цилиндрическом сердечнике. Такая конструкция позволяет получить более точное значение сопротивления, а также увеличивает величину сопротивления. Углеродные пленочные резисторы намного точнее, чем углеродные композиционные резисторы. В приложениях, требующих стабильности на высоких частотах, используются специальные углеродные пленочные резисторы.






