Сборник задач по электротехнике с решениями. Учебное пособие
В первое время после включения показаний амперметра в цепи обмотки I1 = 1,2 А, а после нагрева обмотки до установившейся температуры I2 = 1 А. Учитывая, что температура воздуха в помещении 20 °С
| и | температурный | коэффициент | сопротивления | меди | |||||
| 4 10–3 K–1, найти температуру обмотки. | |||||||||
| 1.1.15) Определить сопротивление проводов воздушной линии при температурах +40 и –40 °С. Дли- | |||||||||
| на линии l = 28,5 км, диаметр медных проводов d = 5 мм. | |||||||||
| 1.1.16) Приемник | за | пять | суток | непрерывной | работы | израсходовал | |||
| 24 кВт ч электроэнергии при напряжении 220 В. Определить ток и сопротивление приемника. | |||||||||
| 1.1.17) Определить плотность тока в проводах диаметром 4 мм, соединяющих приемник с генерато- | |||||||||
| ром. Суточная выработка энергии генератора, составляет 48 кВт ч при напряжении U = 220 В. | |||||||||
| U | 1.1.18) Электрическая | цепь | мощностью | P | = | 5 | кВт | при | напряжении |
| = | 220 | В | подключена | к | генератору | с | внутренним | сопротивлением |
Rвт = 0,22 Ом. Определить эдс и кпд генератора.
1.1.19) Механическая мощность электродвигателя постоянного тока 8,5 кВт при напряжении U = 220 В, кпд 85 %. Определить электрическую мощность и ток двигателя.
1.1.20) На изготовление катушки израсходовано 200 м медного провода диаметром 0,5 мм. На какое постоянное напряжение можно включать эту катушку, если допустимая плотность тока j = 2 А/мм2?
1.1.21) Составить схему электрической цепи, в которой к аккумуляторной батарее присоединены три резистора. Один – регулируемый, включен последовательно с группой из двух нерегулируемых, соединенных между собой параллельно. В схеме предусмотреть управление с помощью двухполюсного выключателя, защиту плавкими предохранителями, измерение общего тока в цепи и напряжения на зажимах батареи.
1.1.22) Составить схему электрической цепи, в которой четыре резистора (один из них регулируемый) образуют замкнутый контур в виде четырехугольника. В одной диагонали четырехугольника – гальванический элемент, присоединенный к цепи через однополюсный выключатель, в другой находится гальванометр, который можно включить и выключить кнопочным выключателем.
1.1.23) Составить схему электрической цепи, в которой последовательно включены два нерегулируемых резистора, аккумуляторная батарея и генератор, которые можно включить согласно или встречно. В схеме предусмотреть защиту цепи плавкими предохранителями, измерение тока, измерение напряжения на зажимах батареи и генератора одним вольтметром с помощью переключателя.
1.1.24) Составить схему электрической цепи, в которой генератор постоянного тока и аккумуляторная батарея, включенные параллельно, снабжают энергией внешнюю часть цепи, состоящей из трех нерегулируемых резисторов, включенных также параллельно. Каждый элемент цепи присоединяется к ней однополюсным выключателем. В схеме предусмотреть измерение общего напряжения, тока в каждом источнике и общего тока приемников энергии.
1.1.25) Два генератора постоянного тока, работая круглосуточно на общий приемник, выработали вместе за месяц 96 000 кВт ч энергии. В течение 10 суток этого месяца первый генератор находился в ремонте. За это время счетчик электрической энергии, установленный на линии к приемнику, показал 2 400 кВт ч. Определить мощность и эдс каждого генератора, если амперметр в цепи первого генератора во время работы показывал 500 А, а в цепи второго – 100 А.
1.1.26) Источник электрической энергии имеет в качестве нагрузки реостат с переменным сопротивлением R, эдс источника Е = 24 В, а его внутреннее сопротивление R = 1 Ом. Построить графики зависимости напряжения U на зажимах источника, мощности источника Pи, мощности приемника Pп, кпд источника, мощности потерь внутри источника Pвт от тока в цепи при изменении сопротивления нагрузки от R = ∞ (холостой ход) до R = 0 (короткое замыкание), считая эдс источника постоянной.
1.2ЗАКОН ОМА
1В электрической цепи за положительное направление эдс Е принимается направление, совпадающее с силой, действующей на положительный заряд, т.е. от «–» источника к «+» источника питания.
За положительное направление напряжения U принято направление, совпадающее с направлением действия электрического поля, т.е. от «+» к «–» источника.
Измерение мощности ваттметром
Мощность потребления трехфазного тока измеряют, используя ваттметры. Это может быть специальный ваттметр, для 3-х фазной сети, либо однофазный, включенный по определенной схеме. Современные приборы учета электроэнергии часто выполняются по цифровой схемотехнике. Такие конструкции отличаются высокой точностью измерений, большими возможностями оперирования с входными и выходными данными.

Варианты измерений:
- Соединение «звезда» с нулевым проводником и симметричная нагрузка – измерительный прибор подключается к одной из линий, считанные показания умножаются на три.
- Несимметричное потребление тока в соединении «звезда» – три ваттметра в цепи каждой фазы. Показания ваттметров суммируются;
- Любая нагрузка и соединение «треугольник» – два ваттметра, подключенных в цепь любых двух нагрузок. Показания ваттметров также суммируются.
Полезная информация для начинающего электрика
Как использовать закон Ома на практике
Почти два столетия назад в далеком 1827 году своими экспериментами Георг Ом выявил закономерность между основными характеристиками электричества.
Он изучил и опубликовал влияние сопротивления участка цепи на величину тока, возникающего под действием напряжения. Ее удобно представлять наглядной картинкой.
Любую работу всегда создает трудяга электрический ток. Он вращает ротор электрического двигателя, вызывает свечение электрической лампочки, сваривает или режет металлы, выполняет другие действия.
Поэтому ему необходимо создать оптимальные условия: величина электрического тока должна поддерживаться на номинальном уровне. Она зависит от:
- значения приложенного к цепи напряжения;
- сопротивления среды, по которой движется ток.
Здесь напряжение, как разность потенциалов приложенной энергии, является той силой, которая создает электрический ток.
Если напряжения не будет, то никакой полезной работы от подключённой электрической схемы не произойдёт из-за отсутствия тока. Эта ситуация часто встречается при обрыве, обломе или отгорании питающего провода.
Сопротивление же решает обратную для напряжения задачу. При очень большой величине оно так ограничивает ток, что он не способен совершить никакой работы. Этот режим применяется у хороших диэлектриков.
Примеры из жизни
Между контактами образуется воздушный зазор. Он отличный изолятор, исключающий движение тока по осветительному прибору.
Ток КЗ способен сжечь электропроводку, вызвать пожар в квартире. Поэтому от таких ситуаций существует только одно спасение: использование защит, способных максимально быстро отключить питающее напряжение.
Для бытовой сети это функция автоматических выключателей или предохранителей, о работе которых я буду рассказывать в других статьях.
Используя сопротивление, следует понимать, что оно, само по себе, не вечно: обладая резервом противостояния приложенной энергии, оно может его израсходовать, не справиться со своей задачей и сгореть.
Поэтому для сопротивления вводится понятие мощности рассеивания, которая надежно отводится во внешнюю среду. Если тепловая энергия, развиваемая прохождением тока, превышает эту величину, то сопротивление сгорает.
Что такое участок цепи
Рассмотрим самую простую электрическую схему, состоящую из батарейки, лампочки и проводов. В ней циркулирует электрический ток.
Представленная схема или полная цепь состоит из двух контуров:
- Внутреннего источника напряжения.
- Внешнего участка: лампочки с подключенными проводами.
Параллельное соединение
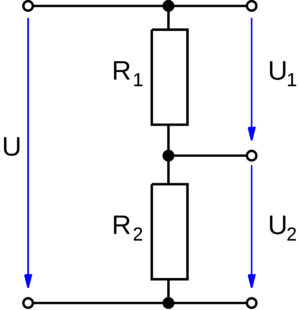 Такое соединение резисторов получается путём объединения двух и более электрических устройств, при котором их одни выводы соединяются друг с другом и образовывают первую общую точку, а другие, аналогично первым, образовывают вторую общую точку. В этом случае напряжение на всех элементах одинаковое, а проходящая сила тока зависит от их импеданса.
Такое соединение резисторов получается путём объединения двух и более электрических устройств, при котором их одни выводы соединяются друг с другом и образовывают первую общую точку, а другие, аналогично первым, образовывают вторую общую точку. В этом случае напряжение на всех элементах одинаковое, а проходящая сила тока зависит от их импеданса.
Формула параллельного соединения резисторов выглядит следующим образом:
R = (R1*R2*R3…*Rх) / (R1+R2+R3…+Rх), где Rх – порядковый номер резистора.
Отсюда следует, что сила тока, протекающая через каждый проводник, находится по формуле: In = U/Rn.
Исходя из этого, при параллельном соединении результирующий импеданс двух и более резисторов будет меньше самого меньшего значения сопротивления в соединении. При этом когда параллельно включены только два резистора, имеющие одинаковый номинал, то их можно заменить эквивалентом, равным одной второй от величины этого номинала.
Так можно соединить и сотню резисторов, тогда эквивалентное сопротивление определяется как сотая часть от номинала. Например, пусть будет участок схемы с десятью резисторами, включёнными параллельно друг другу с номиналом каждого равного 10 Ом, тогда общее сопротивление будет составлять десятую часть, а именно Rоб = 10/10 = 1 Ом.
https://youtube.com/watch?v=Gr2MQcV_zJc
Пример подбора замены
При разработке прибора возникла потребность использовать на участке цепи резистор с сопротивлением 6 Ом. При изучении номинального ряда стандартных значений, выпускаемых промышленностью, можно отметить, что резистора на 6 Ом в нём нет.
Для получения нужного значения понадобится воспользоваться параллельным включением двух элементов. Эквивалентное значение сопротивления для двух резисторов в таком случае находится в следующем порядке:
- 1/R = (1/R1) + (1/R2);
- 1/R = (R1+R2) / (R1*R2);
- Rэ = (R1*R2) / (R1+R2).
Из решения видно, что если R1 совпадает по номиналу с R2, то общая величина сопротивления равна половине значения одного из элементов. Поэтому при требуемом номинале, равном 6 Ом, это значение составит: Rx = 2*6 = 12 Ом. Для проверки результата следует подставить полученный ответ в формулу: Rэ = (R1*R2) / (R1+R2) = (12*12) / (12+12) = 6 Ом.
Задача на нахождение эквивалента
Пусть существует схема с тремя параллельно включёнными резисторами и для её упрощения необходимо заменить их одним элементом. Номиналы проводников составляют: R1 = 320 Ом, R2= 10 Ом, R3 = 1 кОм. Для решения задачи используется уже известная формула:
- 1/R = (1/R1) + (1/R2) + (1/R3);
- Rэкв = (R1*R2*R3) / (R1+R2+R3).
Перед тем как подставлять величины в формулу, их все понадобится привести к международной системе единиц (СИ). Так, один килоОм равен 1000 Ом, при подставлении этого значения получается ответ: Rэ = (320*1*1000) / (320+10+1000) = 2406 Ом или 2,4 кОм, что как раз соответствует величине из стандартного ряда. Такая методика расчёта применяется для любого количества параллельно соединённых резисторов.
Расчёт мощности по току и напряжению
Данный расчет происходит по факту мощности, проделывать его необходимо еще до начала проектирование своего жилища (дома, квартиры).
- Из этого значение зависят кабеля питающие приборы которые подключены к электросети.
- По формуле можно вычислить силу тока, для этого понадобиться взять точное напряжение сети и нагрузку питающихся приборов. Ее величина дает нам понять площадь сечение жил.
Если вам известны все электроприборы, которые в будущем должны питаться от сети, тогда можно легко сделать расчеты для схемы электроснабжение. Эти же расчеты можно выполнять и для производственных целей.
Однофазная сеть напряжением 220 вольт
Формула силы тока I (A — амперы):
Где P — это электрическая полная нагрузка (ее обозначение обязательно указывается в техническом паспорте данного устройства), Вт — ватт;
U — напряжение электросети, В (вольт).
В таблице представлены стандартные нагрузки электроприборов и потребляемый ими ток (220 В).
| Электроприбор | Потребляемая мощность, Вт | Сила тока, А |
| Стиральная машина | 2000 – 2500 | 9,0 – 11,4 |
| Джакузи | 2000 – 2500 | 9,0 – 11,4 |
| Электроподогрев пола | 800 – 1400 | 3,6 – 6,4 |
| Стационарная электрическая плита | 4500 – 8500 | 20,5 – 38,6 |
| СВЧ печь | 900 – 1300 | 4,1 – 5,9 |
| Посудомоечная машина | 2000 — 2500 | 9,0 – 11,4 |
| Морозильники, холодильники | 140 — 300 | 0,6 – 1,4 |
| Мясорубка с электроприводом | 1100 — 1200 | 5,0 — 5,5 |
| Электрочайник | 1850 – 2000 | 8,4 – 9,0 |
| Электрическая кофеварка | 6з0 — 1200 | 3,0 – 5,5 |
| Соковыжималка | 240 — 360 | 1,1 – 1,6 |
| Тостер | 640 — 1100 | 2,9 — 5,0 |
| Миксер | 250 — 400 | 1,1 – 1,8 |
| Фен | 400 — 1600 | 1,8 – 7,3 |
| Утюг | 900 — 1700 | 4,1 – 7,7 |
| Пылесос | 680 — 1400 | 3,1 – 6,4 |
| Вентилятор | 250 — 400 | 1,0 – 1,8 |
| Телевизор | 125 — 180 | 0,6 – 0,8 |
| Радиоаппаратура | 70 — 100 | 0,3 – 0,5 |
| Приборы освещения | 20 — 100 | 0,1 – 0,4 |
На рисунке вы можете видет схему устройства электроснабжение дома при однофазном подключении к сети 220 вольт.
Схема приборов при однофазном напряжении
Как и показано на рисунке, все потребители должны быть подключены к соответствующим автоматам и счетчику, далее к общему автомату который будет выдерживать общею нагрузку дома. Кабель который будет доводит ток, должен выдерживать нагрузку всех подключенных бытовых приборов.
В таблице ниже показана скрытая проводка при однофазной схеме подключение жилища для подбора кабеля при напряжении 220 вольт.
| Сечение жилы провода, мм 2 | Диаметр жилы проводника, мм | Медные жилы | Алюминиевые жилы | ||
| Ток, А | Мощность, Вт | Ток, А | Мощность, кВт | ||
| 0,50 | 0,80 | 6 | 1300 | ||
| 0,75 | 0,98 | 10 | 2200 | ||
| 1,00 | 1,13 | 14 | 3100 | ||
| 1,50 | 1,38 | 15 | 3300 | 10 | 2200 |
| 2,00 | 1,60 | 19 | 4200 | 14 | 3100 |
| 2,50 | 1,78 | 21 | 4600 | 16 | 3500 |
| 4,00 | 2,26 | 27 | 5900 | 21 | 4600 |
| 6,00 | 2,76 | 34 | 7500 | 26 | 5700 |
| 10,00 | 3,57 | 50 | 11000 | 38 | 8400 |
| 16,00 | 4,51 | 80 | 17600 | 55 | 12100 |
| 25,00 | 5,64 | 100 | 22000 | 65 | 14300 |
Как и показано в таблице, сечение жил зависит и от материала из которого изготовлен.
Трёхфазная сеть напряжением 380 В
В трехфазном электроснабжении сила тока рассчитывается по следующей формуле:
I = P /1,73 U
P — потребляемая мощность в ватах;
U — напряжение сети в вольтах.
В техфазной схеме элетропитания 380 В, формула имеет следующий вид:
I = P /657, 4
Если к дому будет проводиться трехфазная сеть 380 В, то схема подключения будет иметь следующий вид.
В таблице ниже представлена схема сечения жил в питающем кабеле при различной нагрузке при трехфазном напряжении 380 В для скрытой проводки.
| Сечение жилы провода, мм 2 | Диаметр жилы проводника, мм | Медные жилы | Алюминиевые жилы | ||
| Ток, А | Мощность, Вт | Ток, А | Мощность, кВт | ||
| 0,50 | 0,80 | 6 | 2250 | ||
| 0,75 | 0,98 | 10 | 3800 | ||
| 1,00 | 1,13 | 14 | 5300 | ||
| 1,50 | 1,38 | 15 | 5700 | 10 | 3800 |
| 2,00 | 1,60 | 19 | 7200 | 14 | 5300 |
| 2,50 | 1,78 | 21 | 7900 | 16 | 6000 |
| 4,00 | 2,26 | 27 | 10000 | 21 | 7900 |
| 6,00 | 2,76 | 34 | 12000 | 26 | 9800 |
| 10,00 | 3,57 | 50 | 19000 | 38 | 14000 |
| 16,00 | 4,51 | 80 | 30000 | 55 | 20000 |
| 25,00 | 5,64 | 100 | 38000 | 65 | 24000 |
Оптимизированная процедура составления системы
По упрощенной методике поступают следующим образом:
- В уравнениях в левой части записывают произведение суммы всех входящих в контур сопротивлений на контурный ток;
- От полученного выражения вычитаются умноженные на сумму сопротивлений общей ветви соседние контурные токи;
- Справа записывается сумма источников ЭДС контура.
Формальный подход
Формальный подход предполагает матричную форму записи системы уравнений. Для расчетов исходные данные записывают в матричной форме. Используются такие матрицы:
- C – в которой i строк, соответствующих количеству контуров, и j столбцов по количеству ветвей;
- Z – диагональная матрица сопротивлений, количество строк и столбцов которой соответствуют числу веток;
- Ct – транспонированная матрица С;
- I – матрица контурных величин;
- J – матрица источников тока;
- Е – матрица ЭДС.
При составлении матрицы С каждый элемент Сij
- 0, если ветвь j не входит в контур;
- -1, если ветвь входит в контур, направление тока противоположно контурному;
- 1 – то же самое, но направление тока совпадает с контурным.
В матрице Z диагональные элементы равняются сопротивлению участков, остальные приравниваются нулю.
Итоговая формула для расчетов имеет вид:
C∙Z∙Ct∙I=C(Z∙J+E).
Такая форма записи решения в матричной форме показывает, каким образом выполняются действия над составленными матрицами.
Пример системы уравнений
Ниже рассмотрен пример расчета конкретной схемы без учета номиналов элементов.
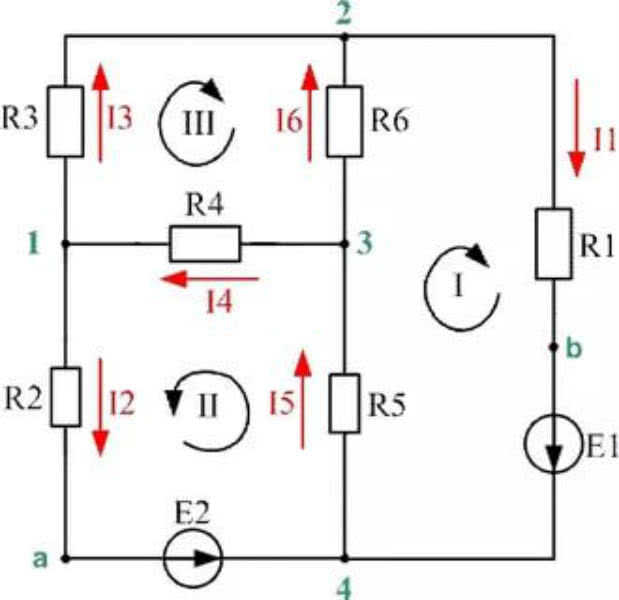
Пример решения
В заданной цепи выделяют три контура. Как выразить токи в ветвях через контурные:
- i1=I1;
- i2=I2;
- i3=I3;
- i4=I2+I3;
- i5=I1+I2;
- i6=I1-I3.
Как составить систему уравнений:
- i1R1+i5R5+i6R6=E1;
- i2R2+i4R4+i5R5=E2;
- i3R3+i4R4-i6R6=0
Как подставить контурные значения
- I1R1+( I1+I2)R5+( I1-I3)R6=E1;
- I2R2+( I2+I3)R4+( I1+I2)R5=E2;
- I3R3+( I2+I3)R4-( I1-I3)R6=0
После преобразования получается необходимая система уравнений:
- (R1+R5+R6)I1+R5I2+R6I3=E1;
- R5I1+(R2+R4+R5)I2+R4I3=E2;
- -R6I1+R4I2+(R3+R4+R6)I3=0.
Система из трех уравнений легко решается после подстановки известных параметров. Из полученных значений контурных токов затем можно найти искомые величины.
Данный пример решения задач по методу контурных токов показывает, что любую достаточно сложную схему можно существенно упростить для решения, руководствуясь указаниями.
Важно! Метод неприменим, если нет возможности преобразовать цепь без взаимного пересечения ветвей. В некоторых случаях упростить схему можно путем преобразования ветвей, соединенных по схеме «звезда» в треугольник
В некоторых случаях упростить схему можно путем преобразования ветвей, соединенных по схеме «звезда» в треугольник.
Точно такие же результаты получаются при использовании метода узловых потенциалов. В основе расчетов – поиск потенциала каждого узла (так называемый узловой потенциал). Существуют программы, позволяющие произвести онлайн расчет параметров по рассмотренным методам.
Расчёт импеданса
Методы вычисления общего сопротивления зависят от способа соединения резисторов. При расчётах общего импеданса за основу берутся законы Кирхгофа.
Так, первый его закон гласит: сумма токов в узле равна нулю. Или, если его перефразировать, значение тока, втекающего в узел, равно сумме токов, вытекающих из этого узла. Второй закон связан с электродвижущей силой, и его формулировка звучит так: сумма разности потенциалов в контуре равна сумме падений разности потенциалов на каждом резисторе в цепи.
При последовательном соединении все элементы располагаются друг за другом без ответвлений. Так как согласно правилу Кирхгофа в любом месте ветви сила тока одинаковая I = I1 = In, то падение напряжения на первом элементе: U1 = I*R1, а на n: Un = I*Rn, где:
- In — сила тока, протекающая через резистор, А.
- Un — значение падения напряжения на резисторе, В.
- Rn — величина сопротивления элемента, Ом.
В результате формула для расчёта сопротивления цепи в этом случае будет выглядеть следующим образом:
Ro = R1 +…+ Rn, где:
- Ro — общее сопротивление ветви.
- R1 — значение импеданса первого элемента.
- Rn — величина сопротивления n-го элемента.
Если цепь параллельная то это значит, что на этом участке несколько ветвей расходятся, а после опять соединяются. Получается, что сила тока в каждой ветви будет своя, а величина напряжения одинакова. Поэтому Uo = U1=…= Un, а Io = I1+…+In. Используя закон Ома, можно записать:
Uo/Ro = U1/R1+…+Un/Rn, или
1/Ro = 1/R1+…1/Rn.
Важные нюансы
 Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности. Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.
Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.
Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.
Видео: Правильное подключение светодиодов
Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения. При этом процедура расчета этого параметра отличается достаточной сложностью, где необходимо учитывать разные параметры.
Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.
Онлайн-расчёт на калькуляторе
 Создано множество интернет-страниц, позволяющих найти сопротивление параллельных резисторов за несколько секунд, используя в своих вычислительных алгоритмах формулы для расчёта параллельного соединения. Такие калькуляторы достаточно полезны радиолюбителям-конструкторам или специалистам РЭА при возникновении затруднения с выбором нужного номинала резистора для замены его в цепи электронного устройства.
Создано множество интернет-страниц, позволяющих найти сопротивление параллельных резисторов за несколько секунд, используя в своих вычислительных алгоритмах формулы для расчёта параллельного соединения. Такие калькуляторы достаточно полезны радиолюбителям-конструкторам или специалистам РЭА при возникновении затруднения с выбором нужного номинала резистора для замены его в цепи электронного устройства.
Внешний вид онлайн-приложений может отличаться друг от друга, а вот принцип работы одинаков. Немаловажным является в работе программ тот факт, что алгоритмы их вычисления используют разную точность в округлении результата, поэтому ответ в некоторых программах при сравнении может немного отличаться.
Само приложение обычно представляет собой ячейки, в которые вносится величина значений резисторов в международной системе измерений. После того как все поля заполнены, нажимается кнопка «Рассчитать» и получается ответ в ячейке напротив. Ответ рассчитывается в Омах. В некоторых приложениях функциональность может быть расширена, это такие возможности, как автоматический перевод значений резисторов в систему СИ, отображение наиближайшего стандартного значения сопротивления из номинального ряда, близкого к полученному ответу.
Полезной функцией может быть и обратный переход, когда вводится эквивалентное сопротивление, а в ответе выдаётся комбинация номиналов проводника для параллельного включения.
https://youtube.com/watch?v=jJX6IsRhnhs
Расчёт сопротивления электрических цепей с использованием законов последовательного и параллельного соединений
Разделы: Физика
Цели:
- Образовательная: систематизировать и закрепить знания учащихся о различных соединениях проводников, сформировать умения применять законы последовательного и параллельного соединений для расчёта электрических цепей, объединить знания, полученные на уроках физики и математики.
- Развивающая: развить мышление учащихся, активизировать познавательную деятельность через решение задач на расчет электрических цепей, развить умение рассчитывать параметры электрических цепей и совершенствовать полученные на уроке навыки.
- Воспитательная: формирование интереса к изучаемому предмету, продолжить формирование коммуникативных умений.
Тип урока: урок проверки и закрепления новых знаний по физике и математике.
Метод проведения урока: практический
Оборудование:
- Громов С.В. Учебник “Физики-9”;
- план урока;
- методика расчета участка электрической цепи постоянного тока;
- карточки-задания.
Сегодня на уроке мы должны применить полученные ранее знания о законах последовательного и параллельного соединений для расчёта участка электрической цепи, а также определить степень усвоения изученного материала с помощью карточек – заданий.
Прежде чем приступить к рассмотрению электрических цепей, вспомним то, что мы уже знаем и ответим на вопросы:
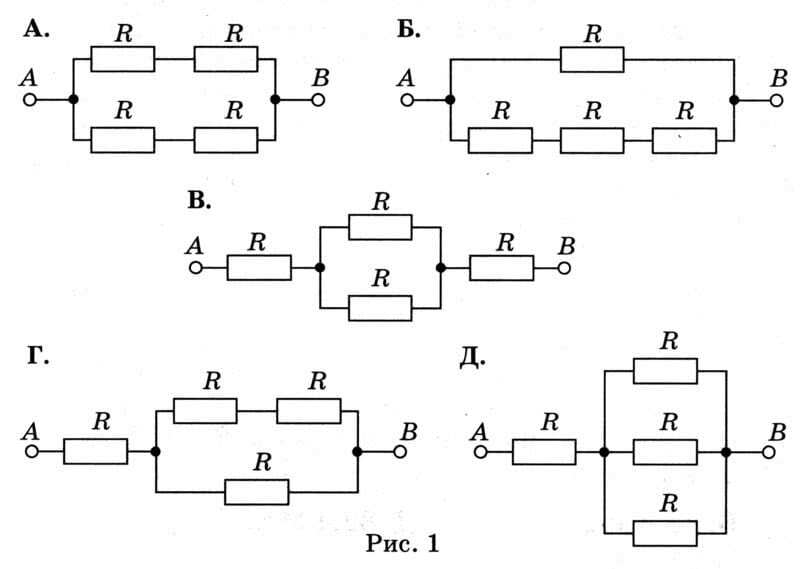
1) Какие виды соединений бывают и как они изображаются на электрических схемах? 2) Назовите законы последовательного соединения? 3) Назовите законы параллельного соединения? 4) Какая отличительная особенность параллельного соединения?
Рассмотрим расчёт участка электрической цепи на примере следующих задач:
1. Рассчитайте общее электрическое сопротивление участка цепи?
1) Наиболее удалённые от источника элементы – это резисторы R2 и R3.
2) Объединяем эти два резистора в первый участок и рассчитываем их общее сопротивление. Резисторы R2 и R3 подключены параллельно, т.к образуют в соединении два узла, следовательно:
Ом
3) Изображаем получившуюся в результате свёртывания резисторы R2 и R3 электрическую схему:
4) Полученные в результате объединения схему с двумя резисторами группируем во второй участок и рассчитываем их общее сопротивление. Так как резисторы R1 и Rоб.1 соединены последовательно, значит:
Ответ: общее сопротивление резисторов на участке электрической цепи 6 Ом.
2. Рассчитайте общее электрическое сопротивление участка цепи?
1) Резисторы R1 и R2 соединены между собой последовательно:
Изобразим полученный электрический участок цепи:
2) Резисторы R3 и R4 соединены между собой последовательно:
Изобразим полученный электрический участок цепи:
3) Полученные в результате объединения схему с двумя резисторами группируем в третий участок и рассчитываем их общее сопротивление. Так как резисторы Rоб.1 и Rоб.2 соединены параллельно, значит:
Ом
Ответ: общее сопротивление резисторов на участке электрической цепи 2,1 Ом.
3. Выполните задания самостоятельно по карточкам (дифференцированные), воспользовавшись памяткой расчета участка электрической цепи постоянного тока:
а) Рассчитайте общее электрическое сопротивление участка цепи?
б) Рассчитайте общее электрическое сопротивление участка цепи?
в) Рассчитайте общее электрическое сопротивление участка цепи?
Сегодня на уроке мы рассмотрели различные схемы участков электрических цепей, научились рассчитывать цепи, применяя законы последовательного и параллельного соединений, а также закрепили полученные знания с помощью карточек – заданий.
Последовательное включение
 Такой вид включения подразумевает вид соединения, когда резисторы соединяются между собой только одним выводом, образовывая цепочку, при этом между её началом и концом отсутствует проводимость, соответствующая режиму короткого замыкания. При использовании последовательного соединения сила тока будет одинакова для любого проводника, а разность потенциалов на участке цепи составит значение равное сумме разностей потенциалов, на выводах каждого из проводников. Расчёт общего значения импеданса в этом случае совсем несложен, для этого просто суммируются все номинальные значения элементов входящих в состав цепочки: Rобщ=R1+R2+…+Rn.
Такой вид включения подразумевает вид соединения, когда резисторы соединяются между собой только одним выводом, образовывая цепочку, при этом между её началом и концом отсутствует проводимость, соответствующая режиму короткого замыкания. При использовании последовательного соединения сила тока будет одинакова для любого проводника, а разность потенциалов на участке цепи составит значение равное сумме разностей потенциалов, на выводах каждого из проводников. Расчёт общего значения импеданса в этом случае совсем несложен, для этого просто суммируются все номинальные значения элементов входящих в состав цепочки: Rобщ=R1+R2+…+Rn.
Например, в схеме применяется цепочка сопротивлений, состоящая из пяти резисторов: R1=32 Ом, R2=16 Ом, R3=1 кОм, R4=4,7 кОм, R5=1 Ом. После приведения всех номиналов к международной системе, получится ответ, равный: Rобщ = 32+16+1000+4700+10=5758 Ом или 5,75 кОм, что соответствует стандартному значению 5,6 кОм.






